机器学习 李宏毅 笔记
Intro
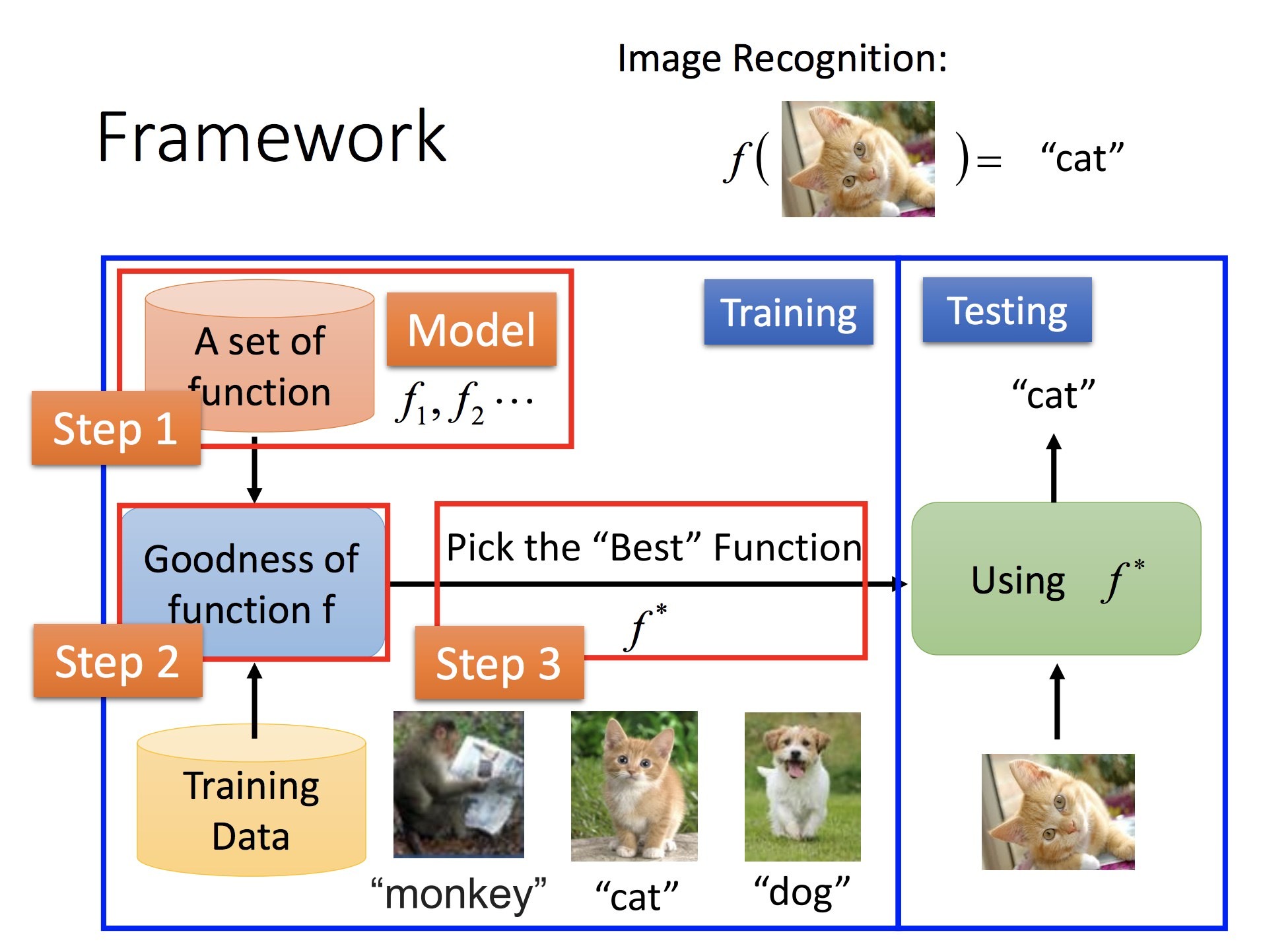

- Supervised Learning: 需要大量 training data
- Structured Learning: 输出具有结构的结果,例如语句

Lecture 1: Regression - Case Study
- Regression: 输出是一个 scalar
妙蛙种子 cp 值的例子
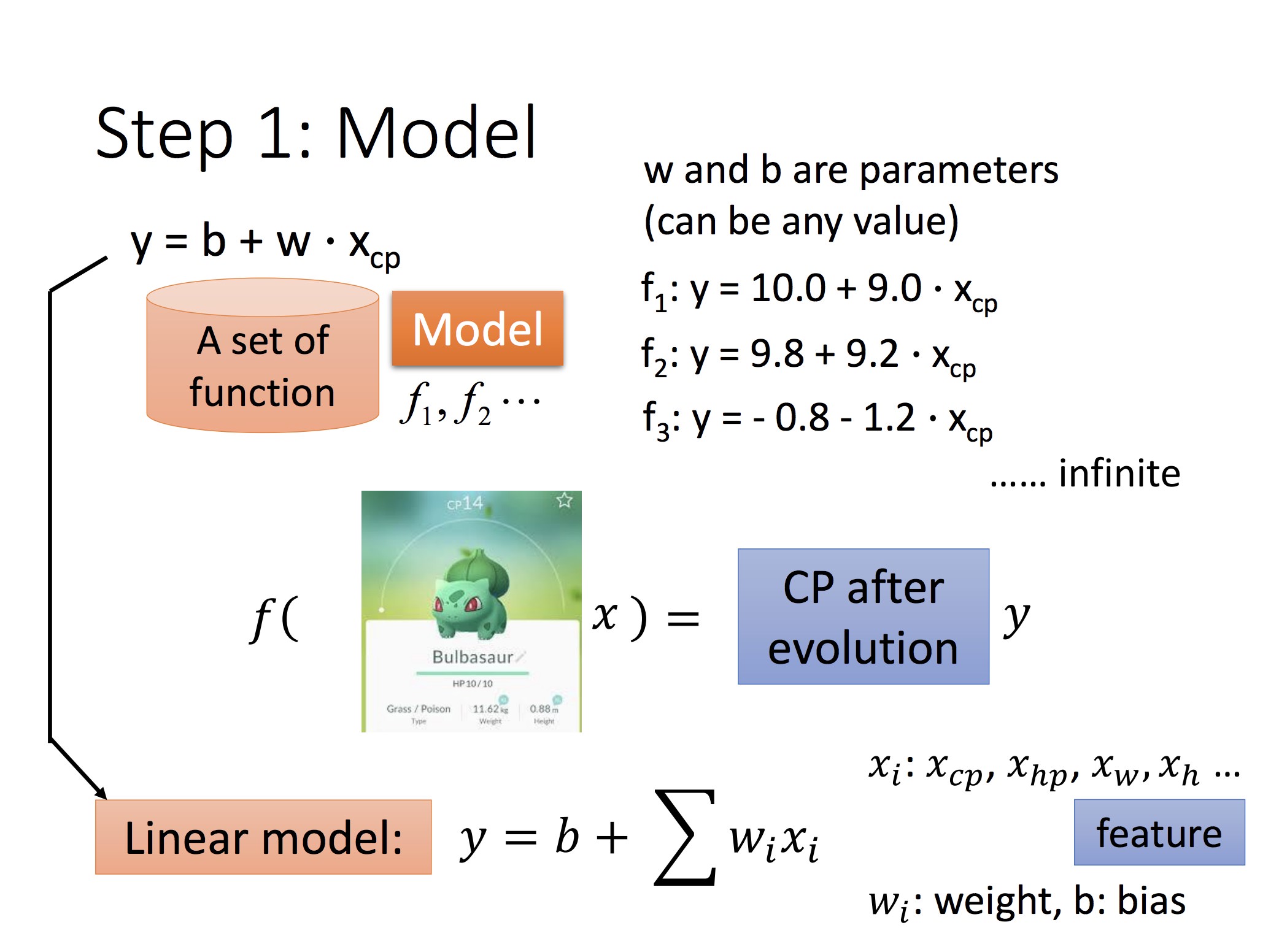
对可微分的 f,可以用梯度下降法解最优(另:这可以直接最小二乘求最优):
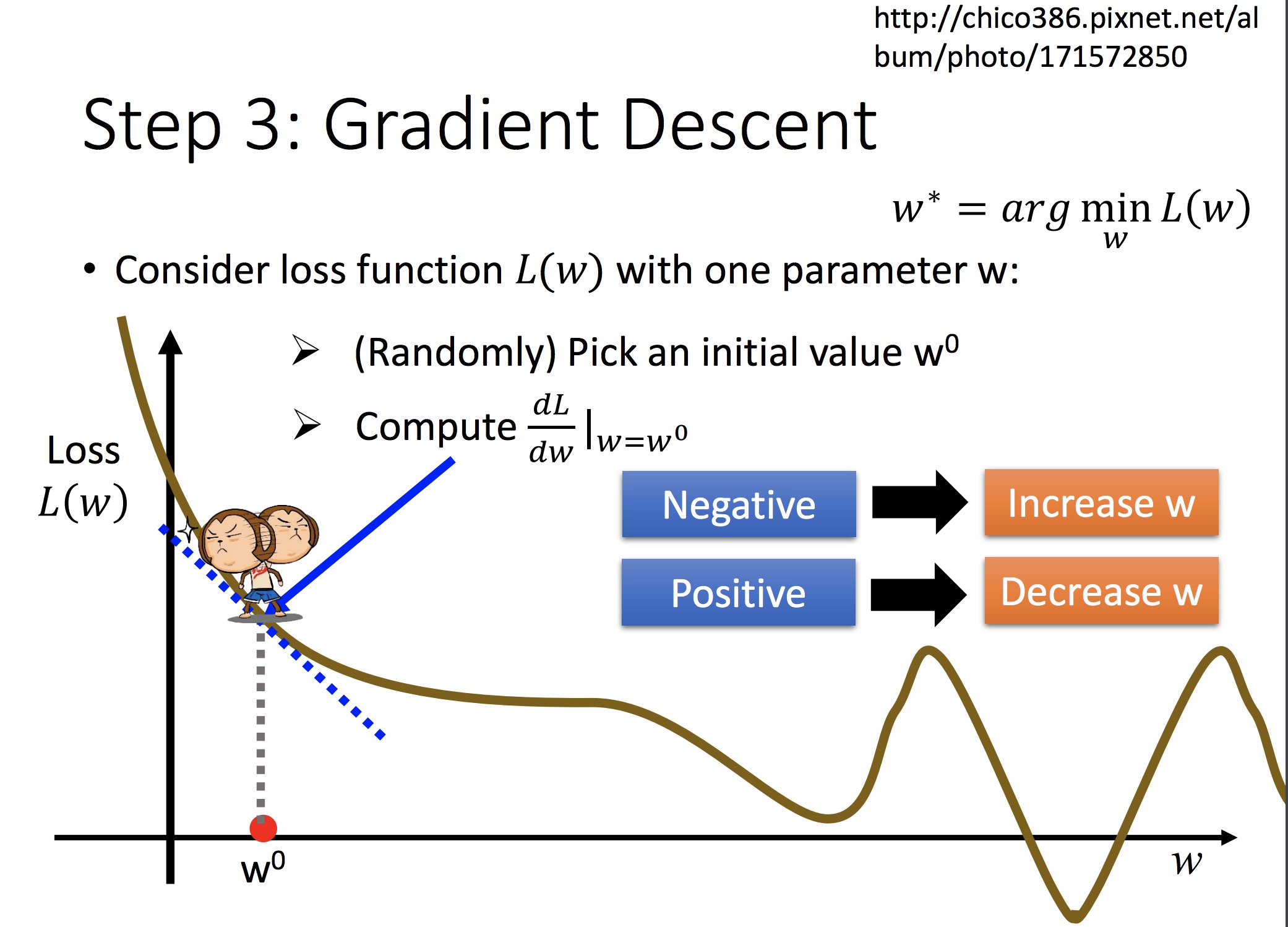
单参数做法:
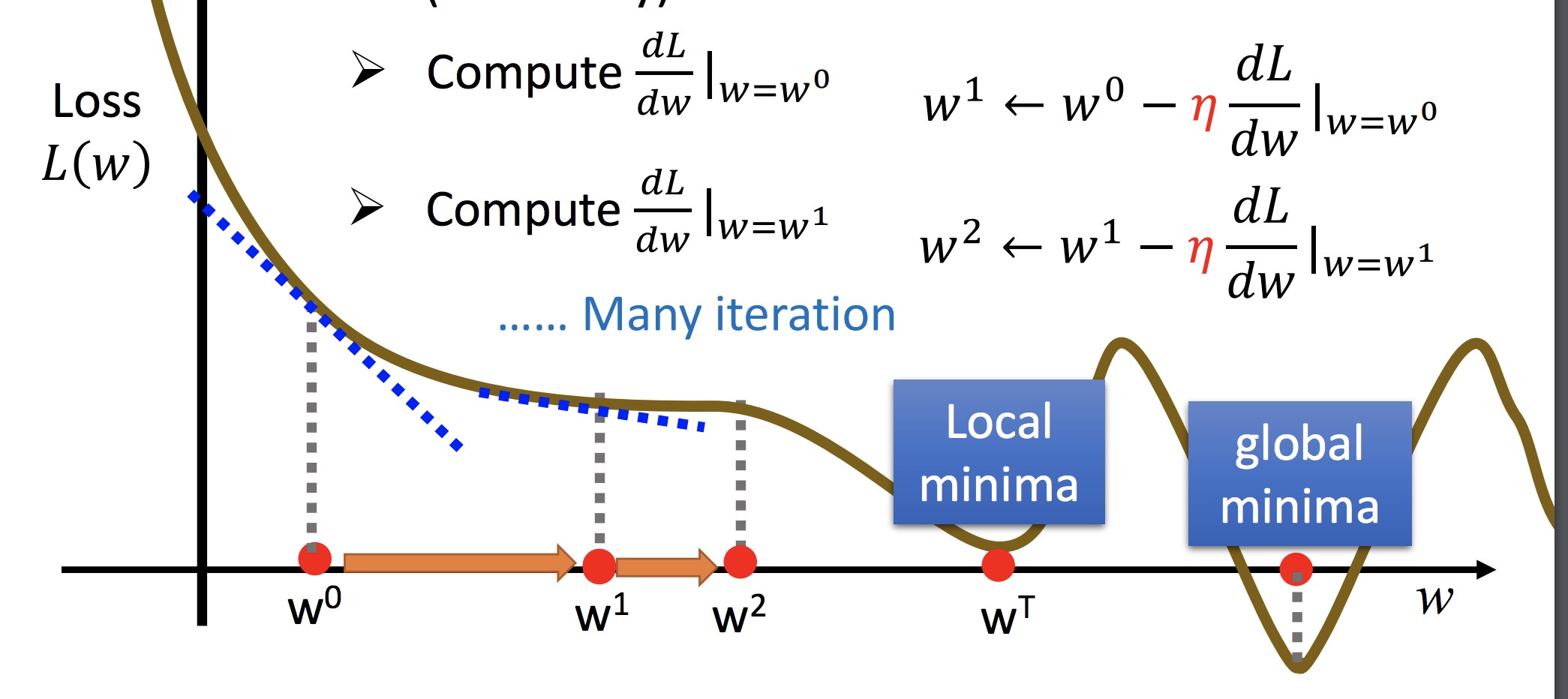
双参数做法:

如此迭代
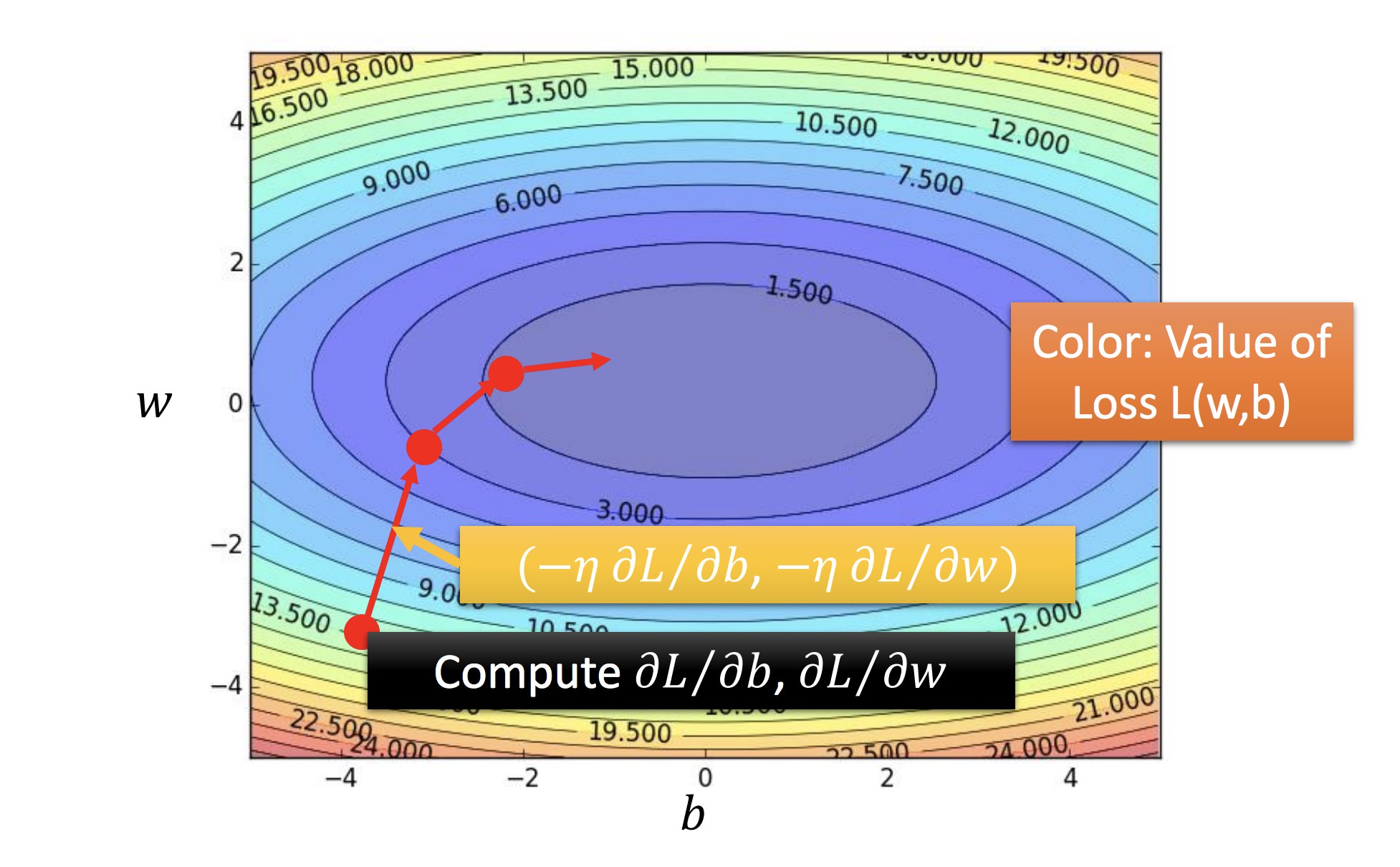
黄色:f 的梯度方向
担心:初始值选取不同可能会陷入不同的鞍点(此时可能只到达局部最优)
在线行回归中不必考虑,因为 Loss Function 是 convex 的
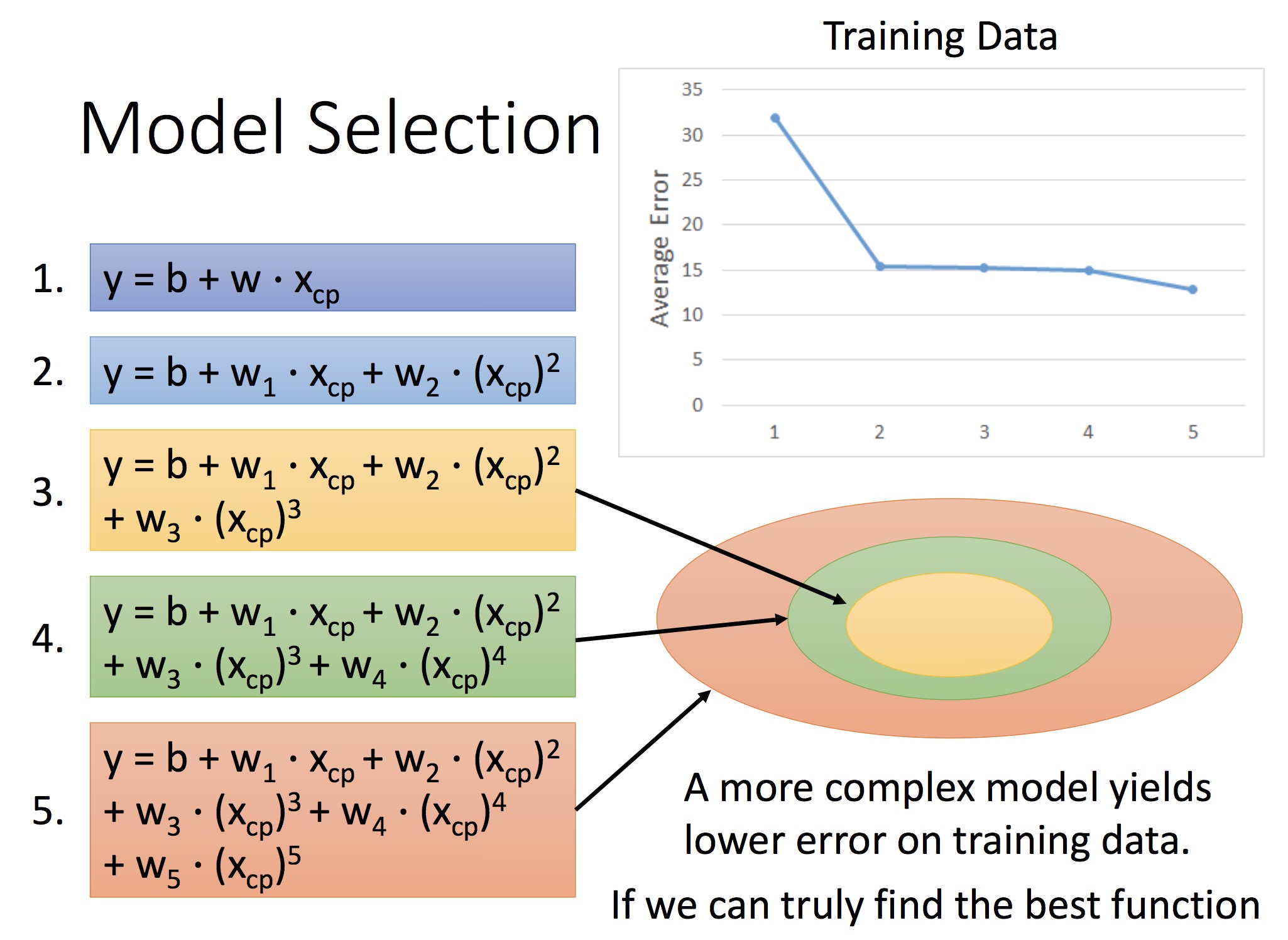
后面讲拟合的误差,以及模型不同导致的拟合误差差异:
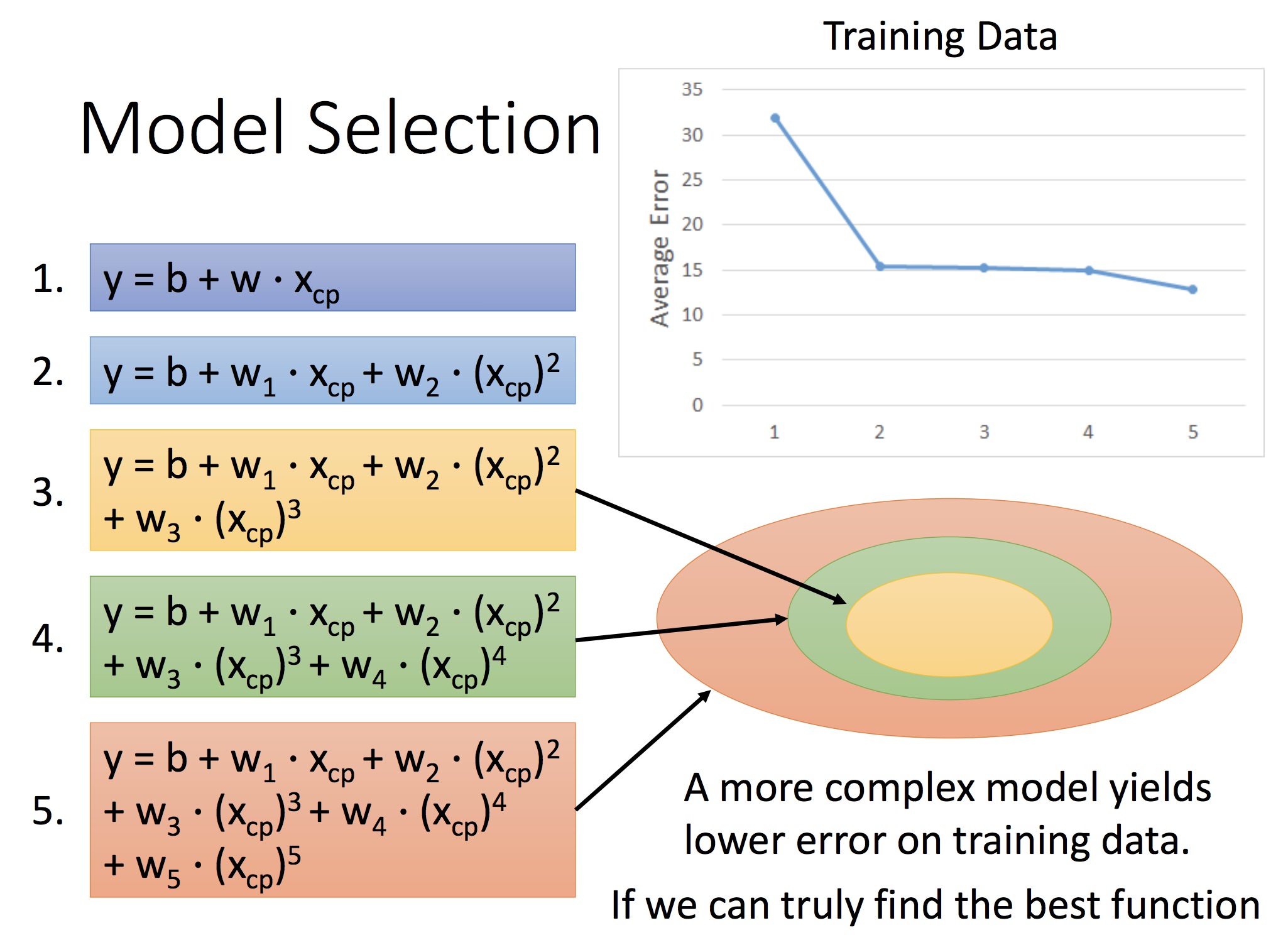
圆圈代表了模型的空间,模型次数越高,空间越大但误差也越大
所以要选择合适的 Model:
再考虑物种的情况,加入 Xs。预测与决策的内容(4-5: 含虚变量的回归)Xs 相当于一个决定截距的虚变量
本节的话除了思想,基本都是很基本的知识.
Regularition
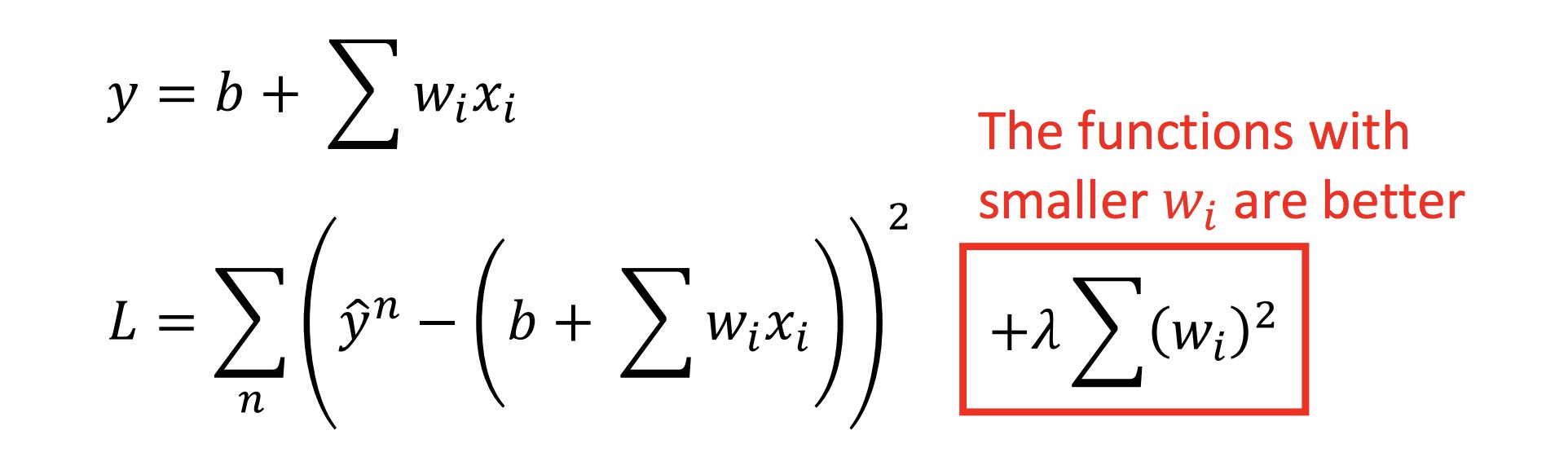
确定 Loss function 时,除开 error 项(第一项),往往加上第二项,这样确定下来的拟合函数系数可以尽量小,函数也会更加平滑:
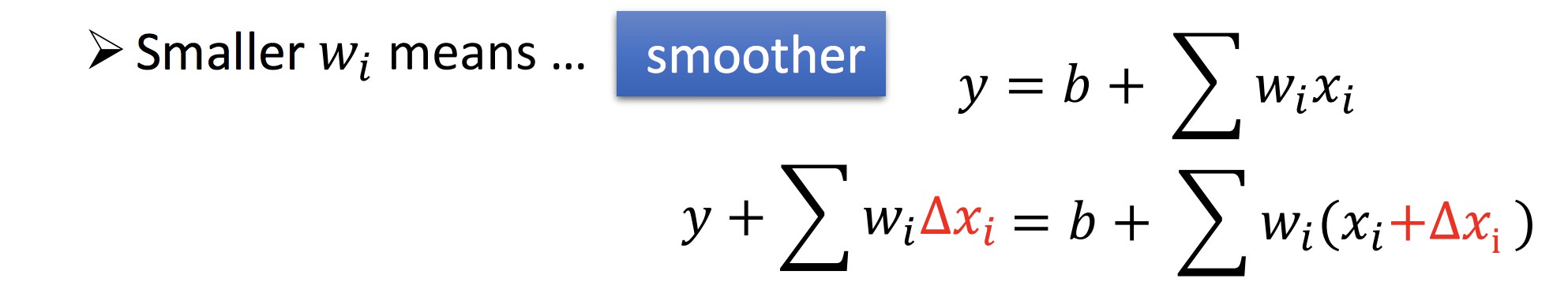
λ 的选取:
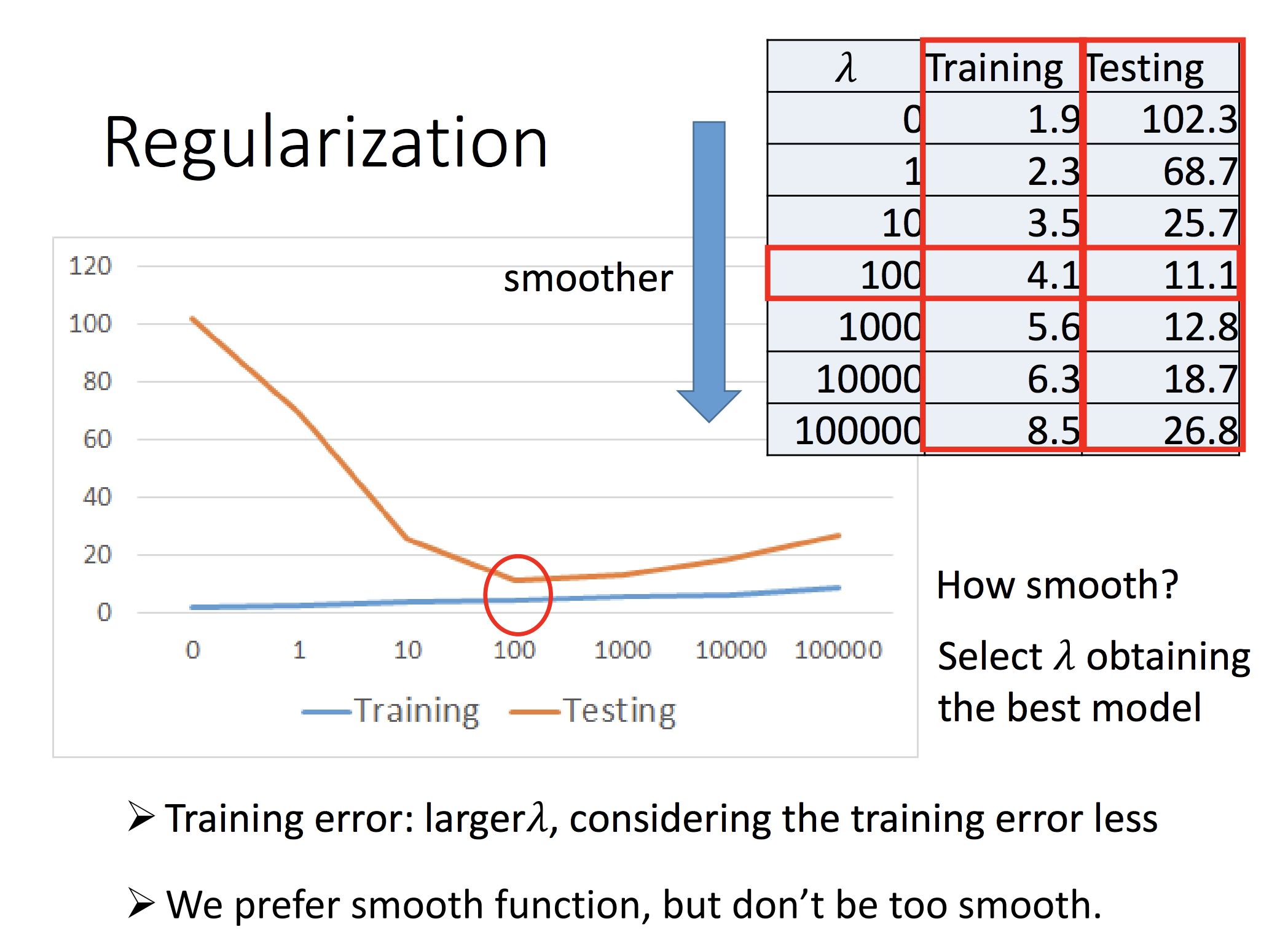
合适即可
总结:

Demo:
演示了梯度下降法逼近最优解的过程
Lecture 2: Error 来源 - Model 选取
数据误差的构成:

表现在 Loss Function 函数上:
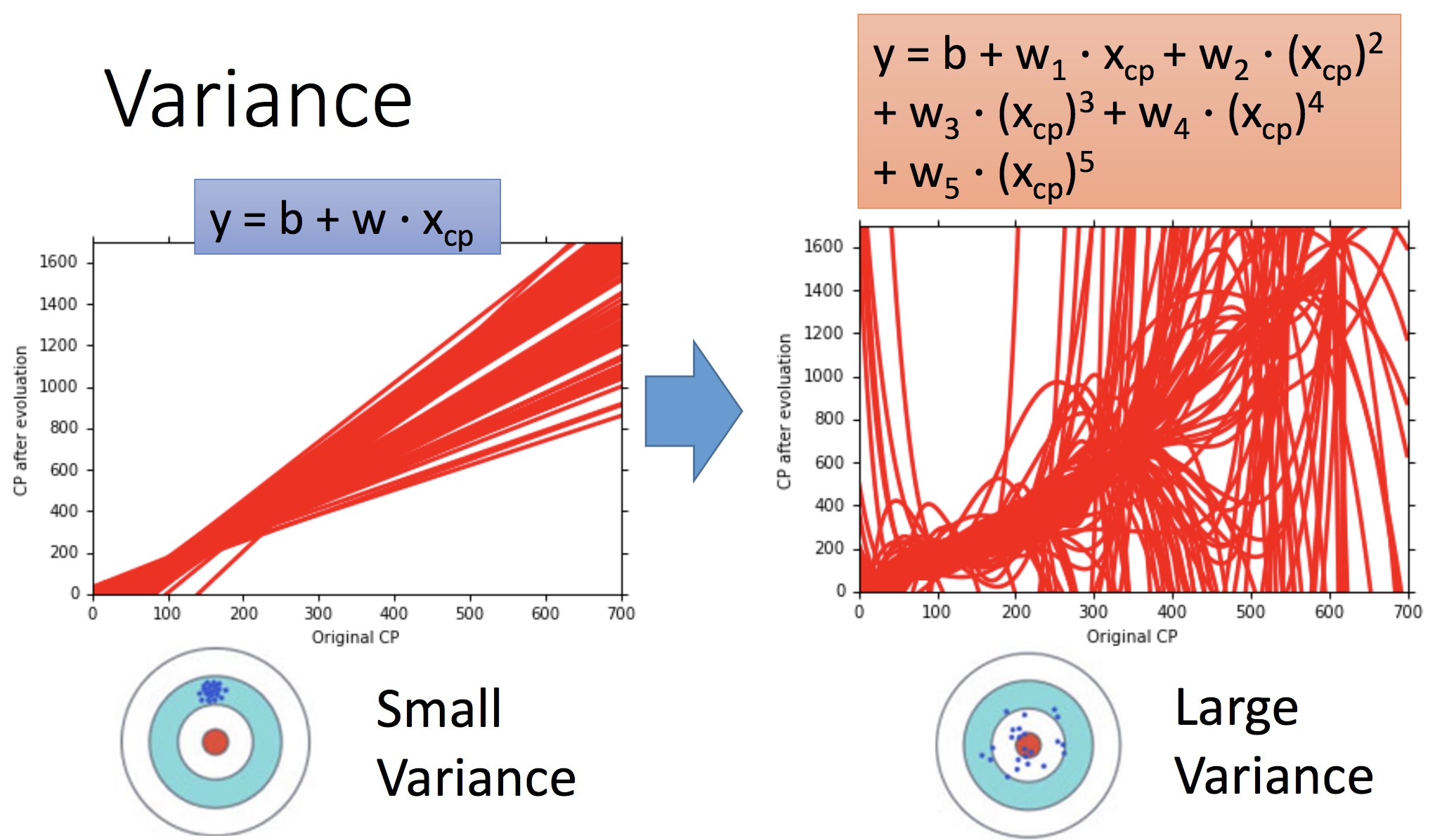
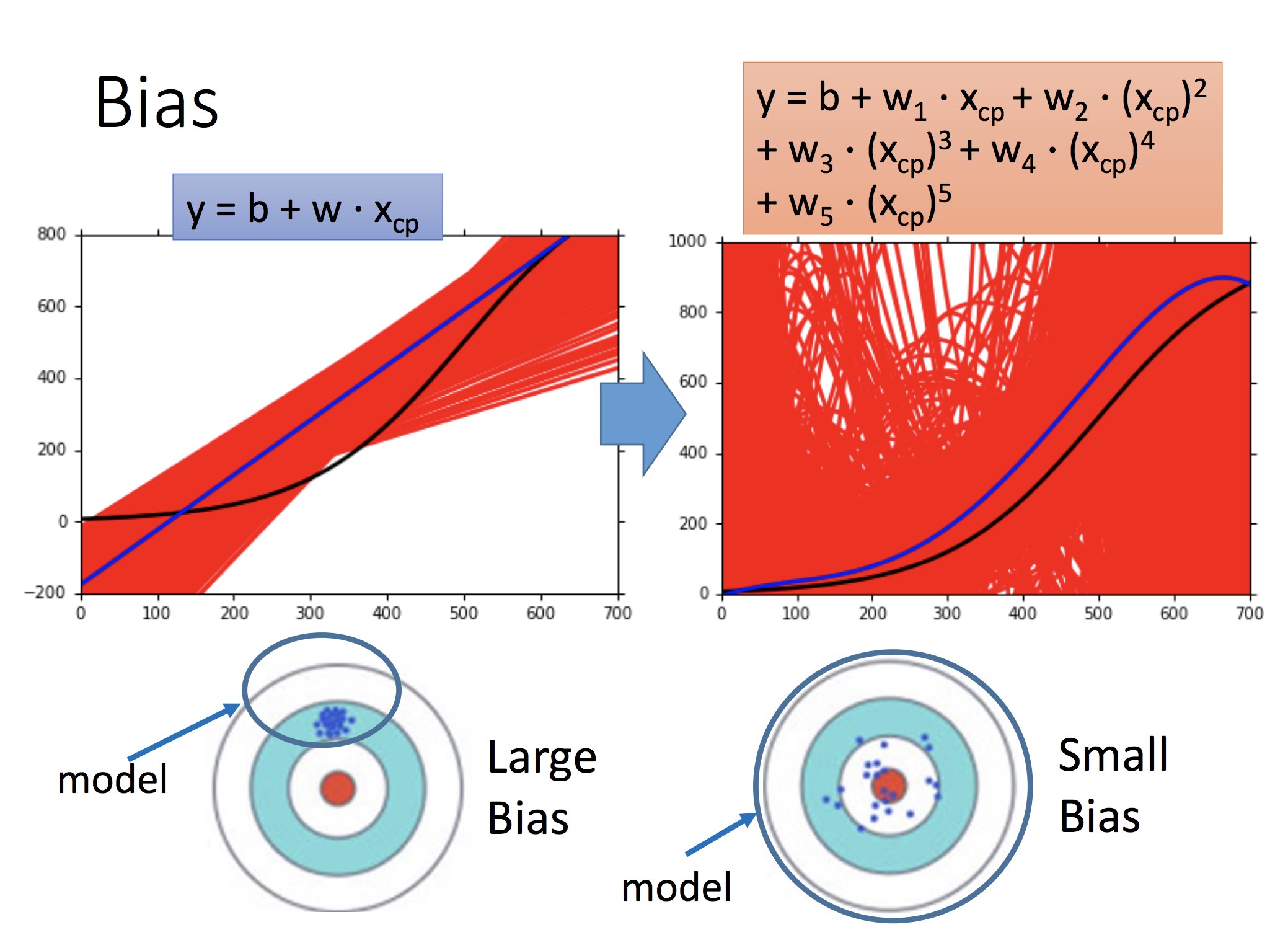
1: 分布较为集中(方差小),但是距离 f hat 还是有距离,偏差较大 = 代表简单的 Model
2: 分布散乱(方差大),但是偏差小 = 代表复杂的 Model
蓝色圈:最初选定的 Model set 集合。例如,采用一次回归注定了这个 set 的偏差较大
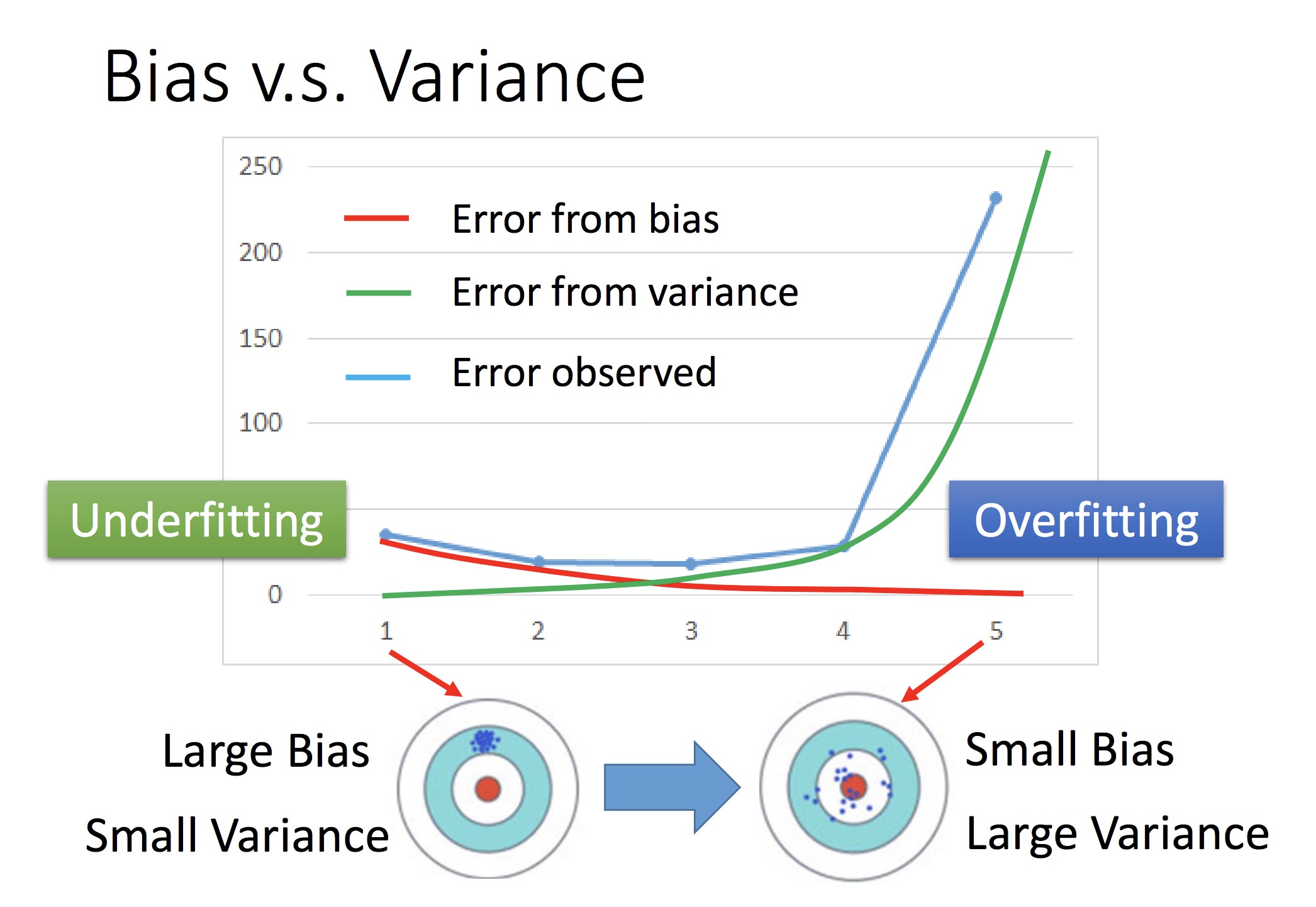
随着模型次数增加,偏差会越来越小(瞄得越来越准),但是分布会更加散乱
同时考虑的时候,可以得到蓝色的线,采取最合适的点代表的模型
如何减小误差
对 Bias:• Add more features as input • A more complex model
简单来讲就是换个好点的模型
对 Var: · 更多的训练数据 · 采用规范化(加上 λ(w𝙞)^2 项)
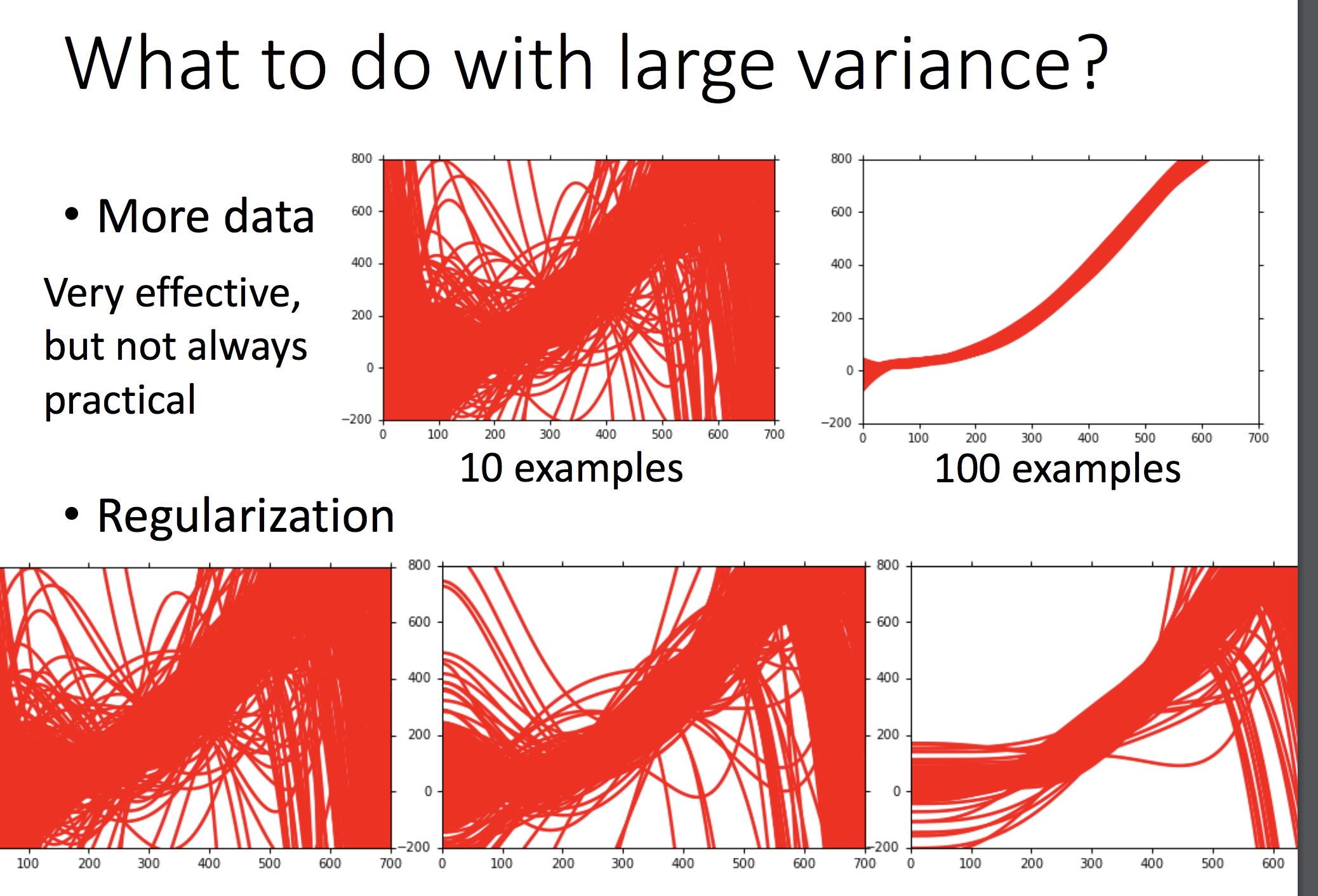
模型的选择上的问题:

不应该:用手上已有的 Testing Set 去评价 model 好坏,因为真正的 Testing Set 全集是我们不具有的,真正的 set 下评价可能会不同
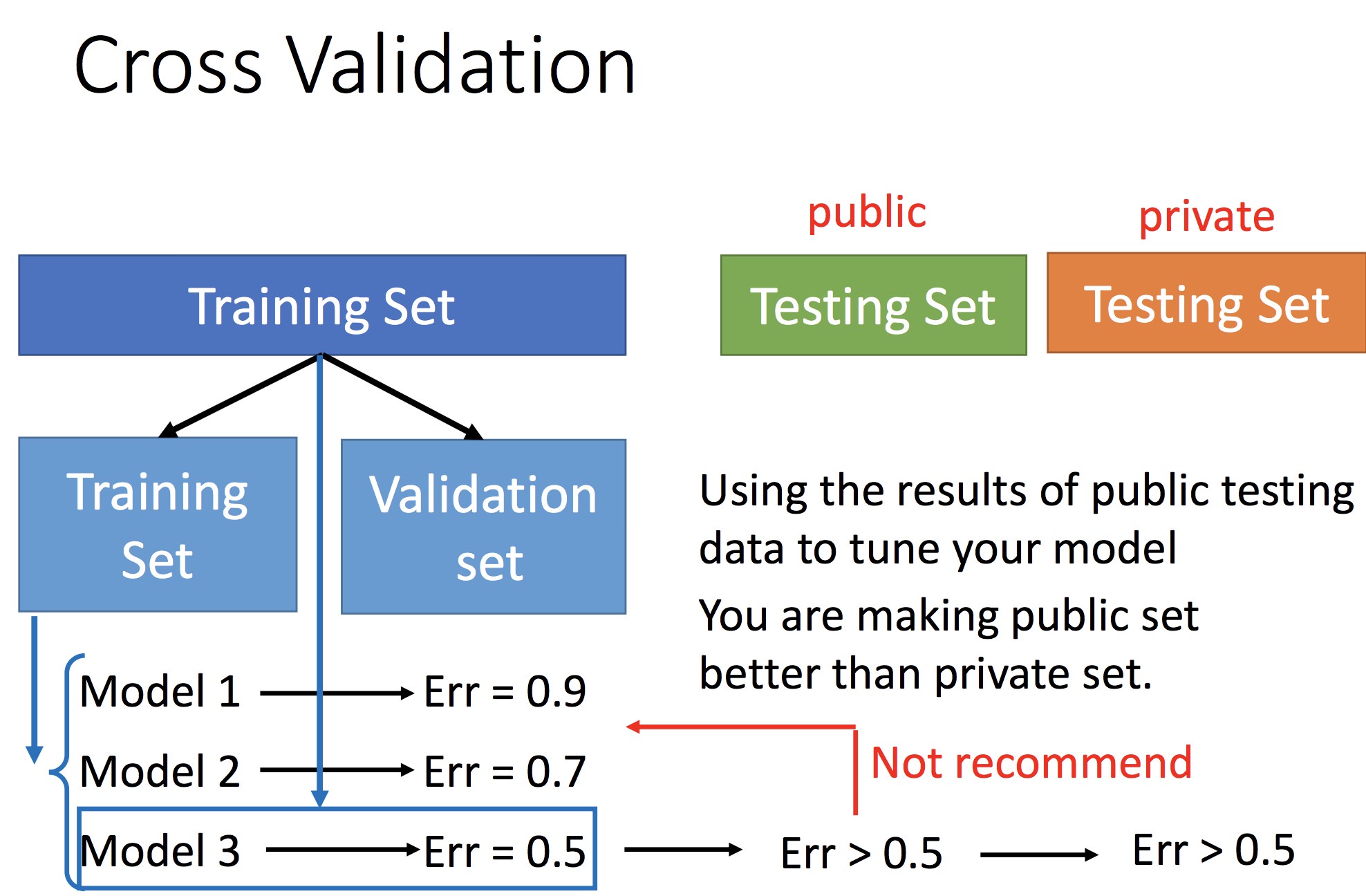
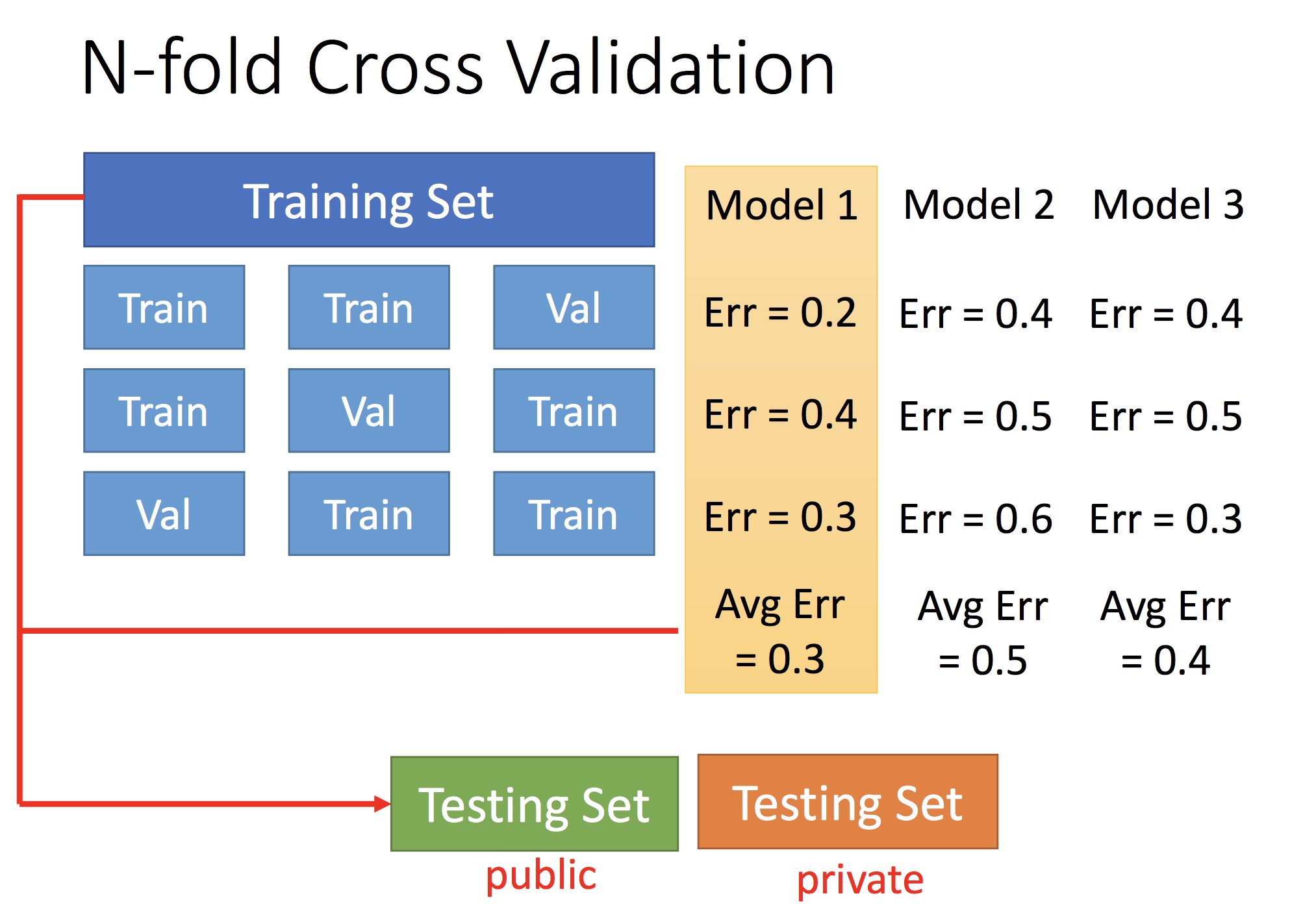
通过交叉验证确定最优 Model
两个 Demo:
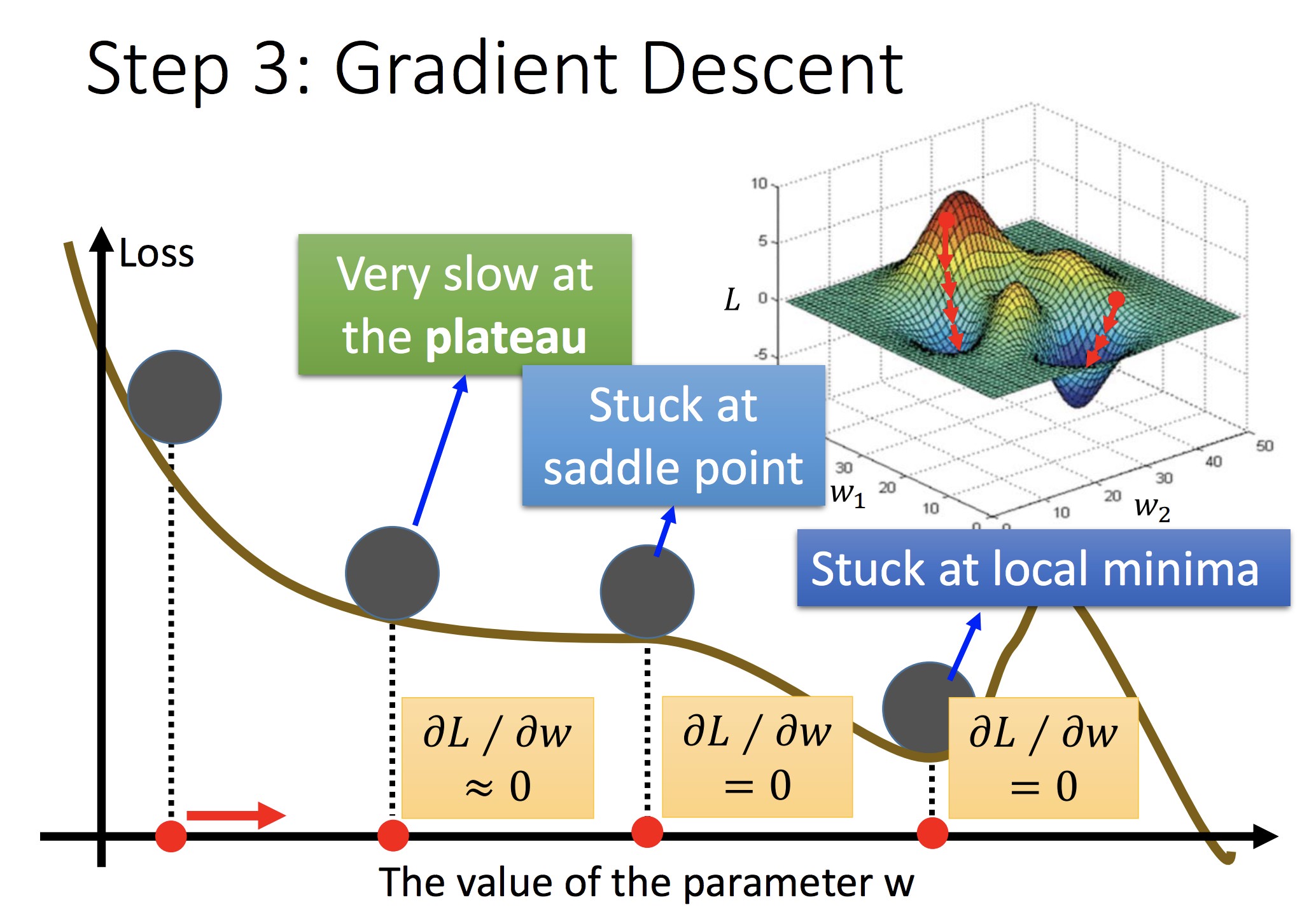
1:表明局部最优和全局最优的关系
2:表明采用梯度下降法,说明存在 f 会不降反增的 case