LTN

2018/3/10 @奉贤海湾

图中的人不是我

1. King’s Cross

f/2.8 1/20s ISO 320 +Extinc 2018/12/18 18:06

摄于国王十字车站一出口。站内还有青烟。

只进行了简单调色

前文地址 (茫茫， Formular 1)

引

前一次写F1相关话题的时候是在13年。当时看了红牛内斗有感而发，加上最喜欢的车手韦伯机长退役。现在五年过去了，14年开始混动时代来临，谁都想不到这五年全部被银箭垄断了。

五年前机械轰鸣更加纯粹，银箭还叫梅赛德斯AMG。

梅赛德斯-奔驰（或是叫梅赛德斯AMG？），同迈凯轮一样，在一二线车队间游走。简森巴顿、汉密尔顿、罗斯伯格、佩雷兹都很有潜力，但都被压制了。送走舒马赫，梅赛德斯的积分说明了它的稳定。

神莲也分家了——路特斯还是莲花？车手无疑是神莲的优势，而且其“硬件”也不错。其长期保持的一二线间的位置更有利于向领奖台冲击——我还是挺支持神莲的。

威廉姆斯无疑是一个悲剧。教授时代的威廉姆斯车队风光无限屡登宝座无人能拦。如今虎落平阳，只有偶尔在事故画面和最后几圈被套圈的让车镜头中看到威廉姆斯了——这样坚持一定很辛苦。

其他的诸如索伯、印度力量、红牛二队也没什么了。不得不说日系主力本田退出F1，小林可梦伟的离开是让人伤心的——街车漂移之都的企业家也无心经营F1了，虽明年本田将以发动机提供商回归。

科技以换壳为本。

十年前乔老爷子从信封里面拿出来了MacBook Air，多少人激动得热泪盈眶。十年前啊。你现在的电脑能放进信封吗。

然后他告诉你，手机是可以触摸的。
还有平板电脑这种产品。

对十年前，现在的技术先进很多倍。但是很少有发布会，能让我们真正“哇”出来的，甚至是苹果自己和谷歌的发布会。我们需要的的确是更强大更好用的产品，但是十年前，十五年前，它就是这样了。所以它们发展到极致也就是那样。

真正能让人“哇”出来的，是那些打破界限，打破思维定式的创新，而不是隐藏刘海这些误入歧途的创新。

总体感受

整体焦段：由于镜头结构和两段式的电动变焦结构，整个焦段表现都没有出现翻车的情况，靠近 70 端改变了变焦结构保证 70 的非球面成像质量，不过实际体验下来 70 端除非特殊要求还真的少用比较好，因为 70 端的光圈和边缘画质非常不稳定，吃光线非常厉害，室内用 70 段经常 ISO 乱飙手动压下来。

Intro

• Supervised Learning: 需要大量 training data
• Structured Learning: 输出具有结构的结果，例如语句

Lecture 1: Regression - Case Study

• Regression: 输出是一个 scalar

妙蛙种子 cp 值的例子

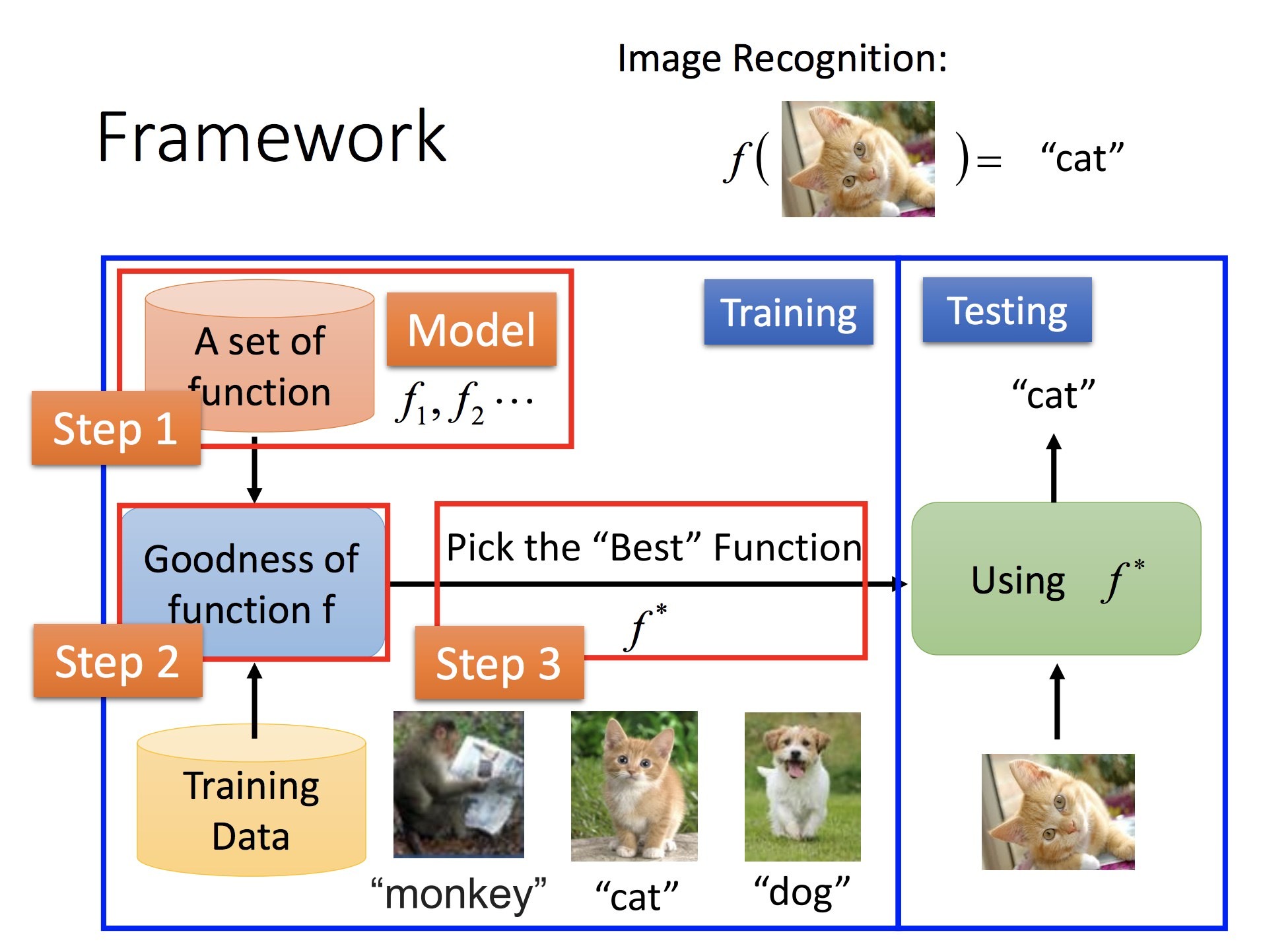
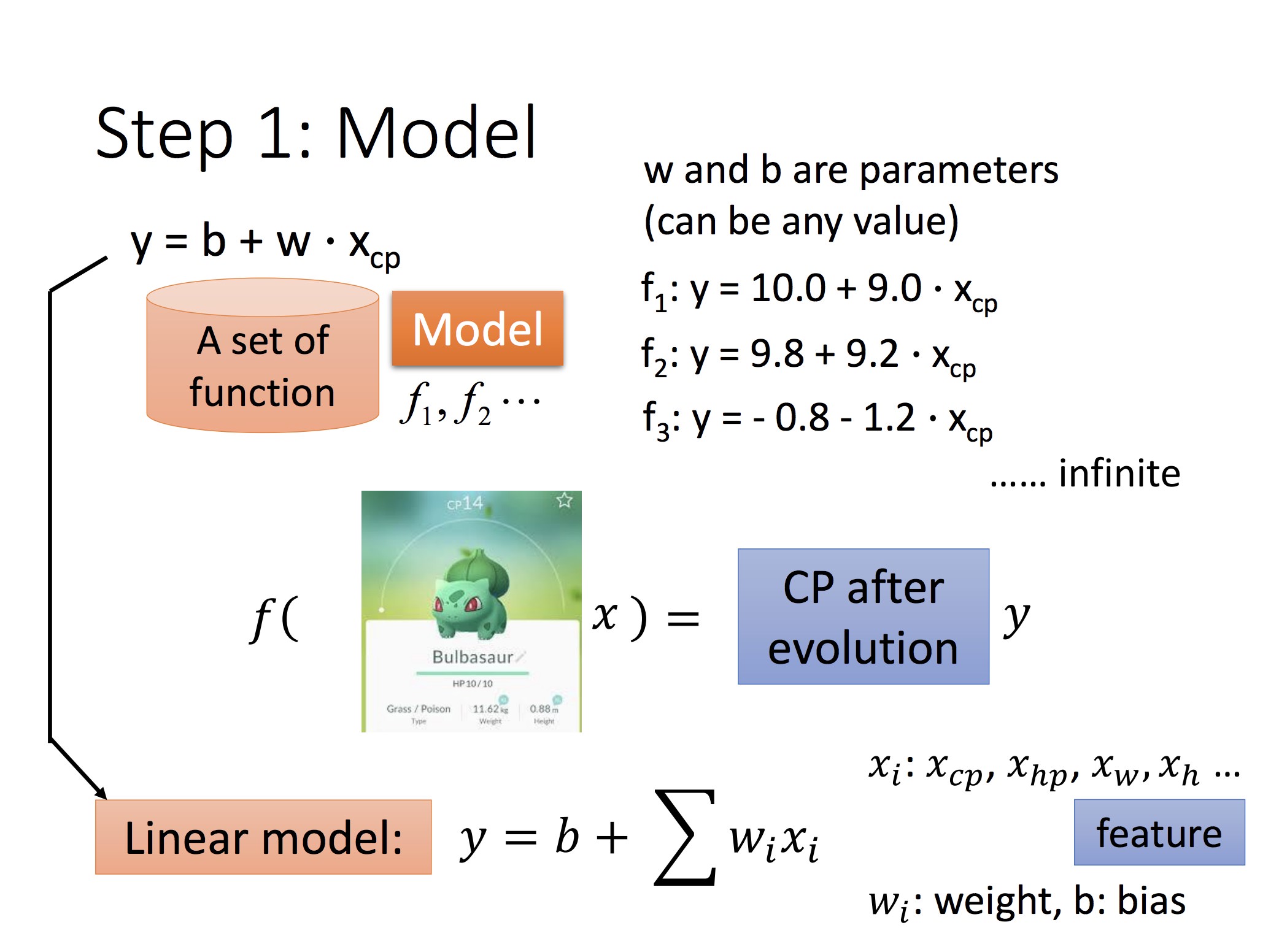
对可微分的 f，可以用梯度下降法解最优（另：这可以直接最小二乘求最优）：

单参数做法：

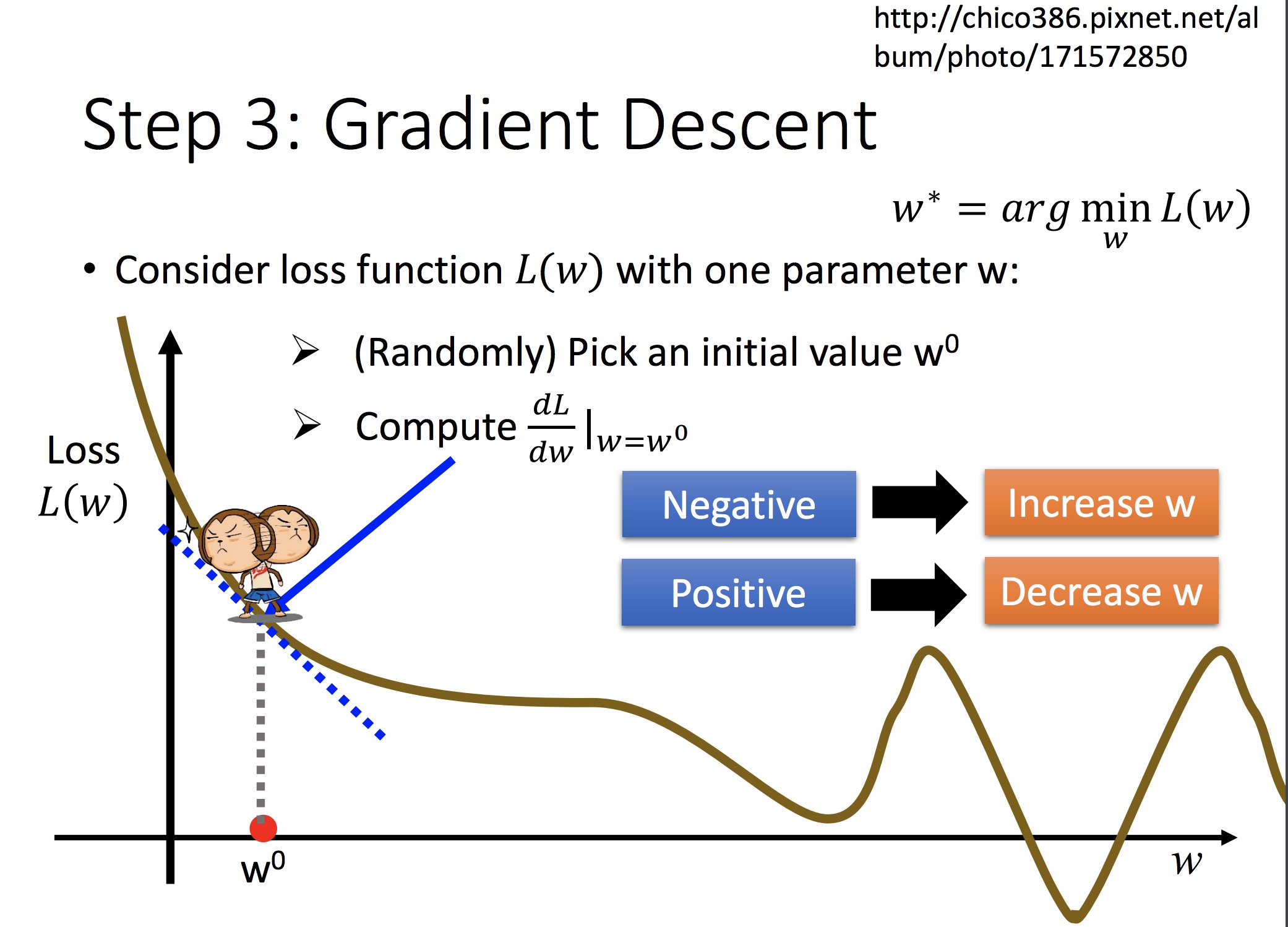
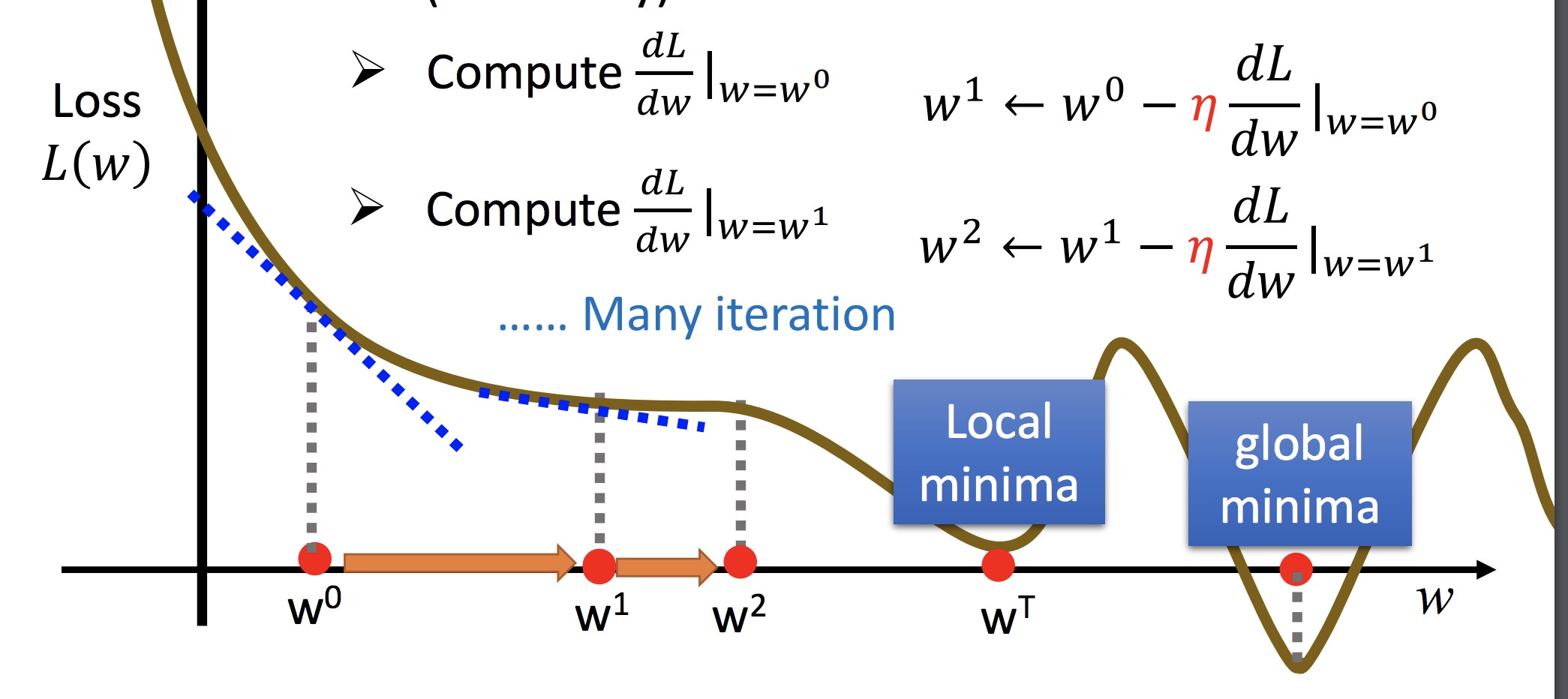
双参数做法：

如此迭代

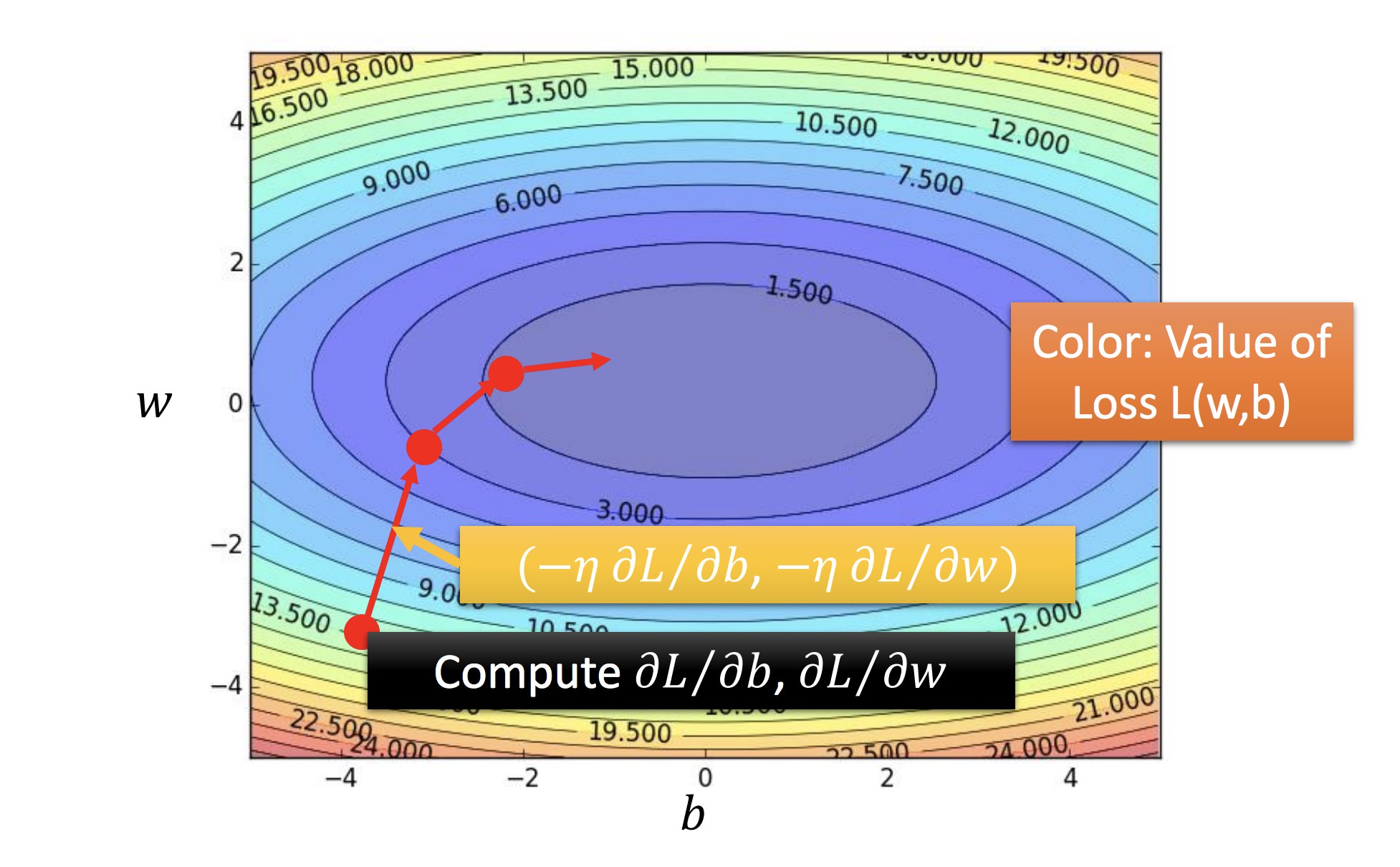
黄色：f 的梯度方向

担心：初始值选取不同可能会陷入不同的鞍点（此时可能只到达局部最优）

在线行回归中不必考虑，因为 Loss Function 是 convex 的

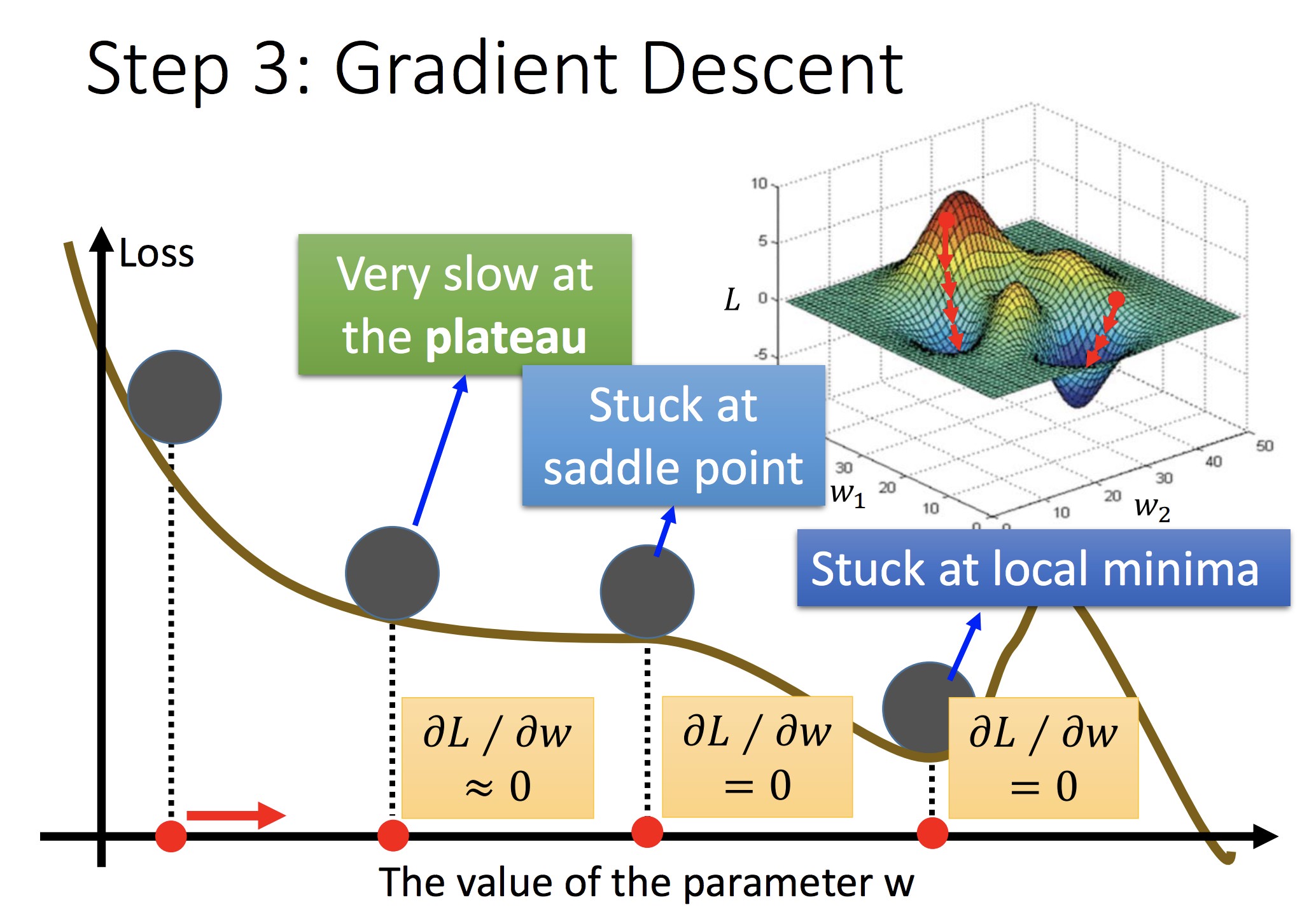
后面讲拟合的误差，以及模型不同导致的拟合误差差异：

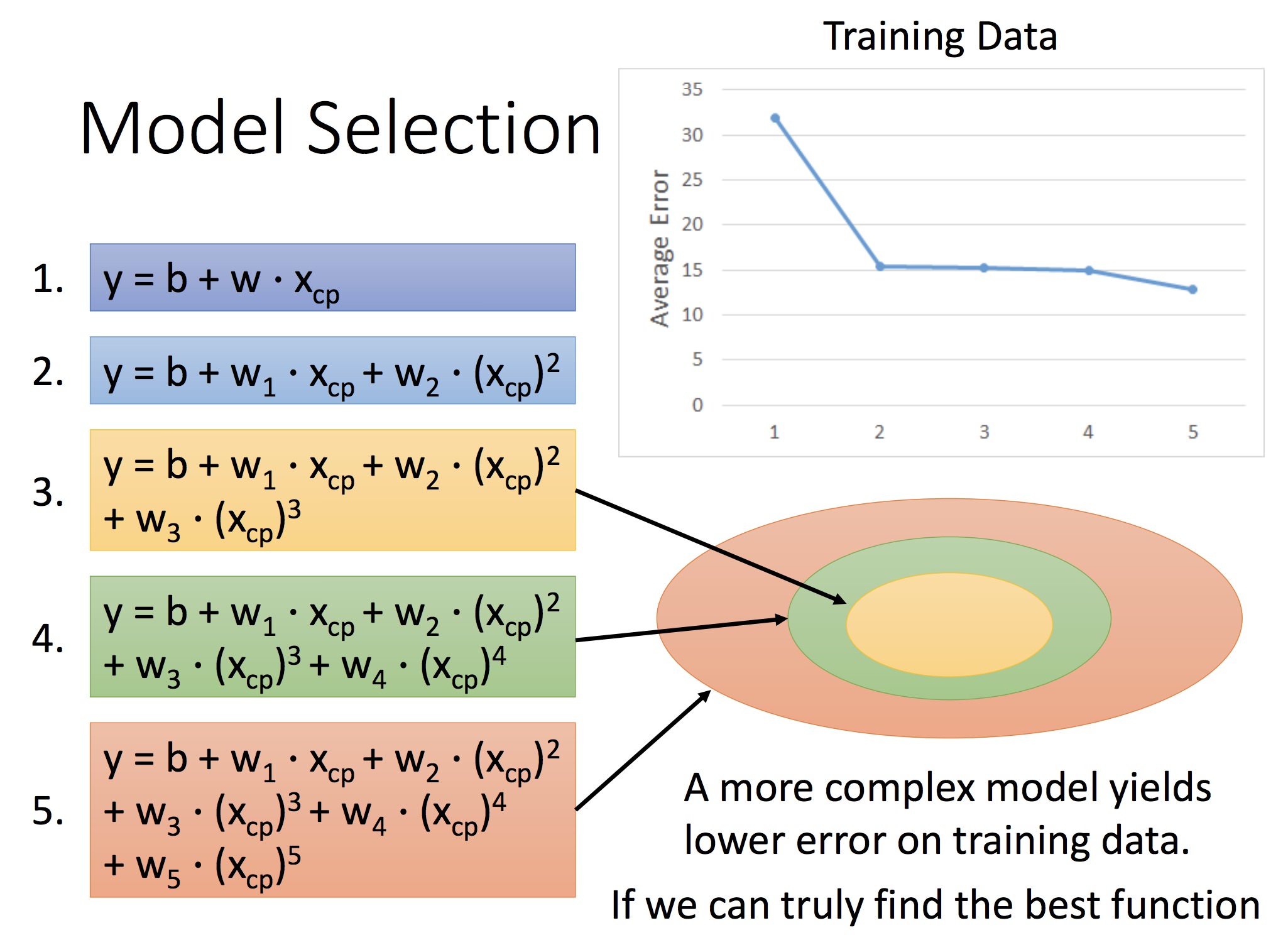
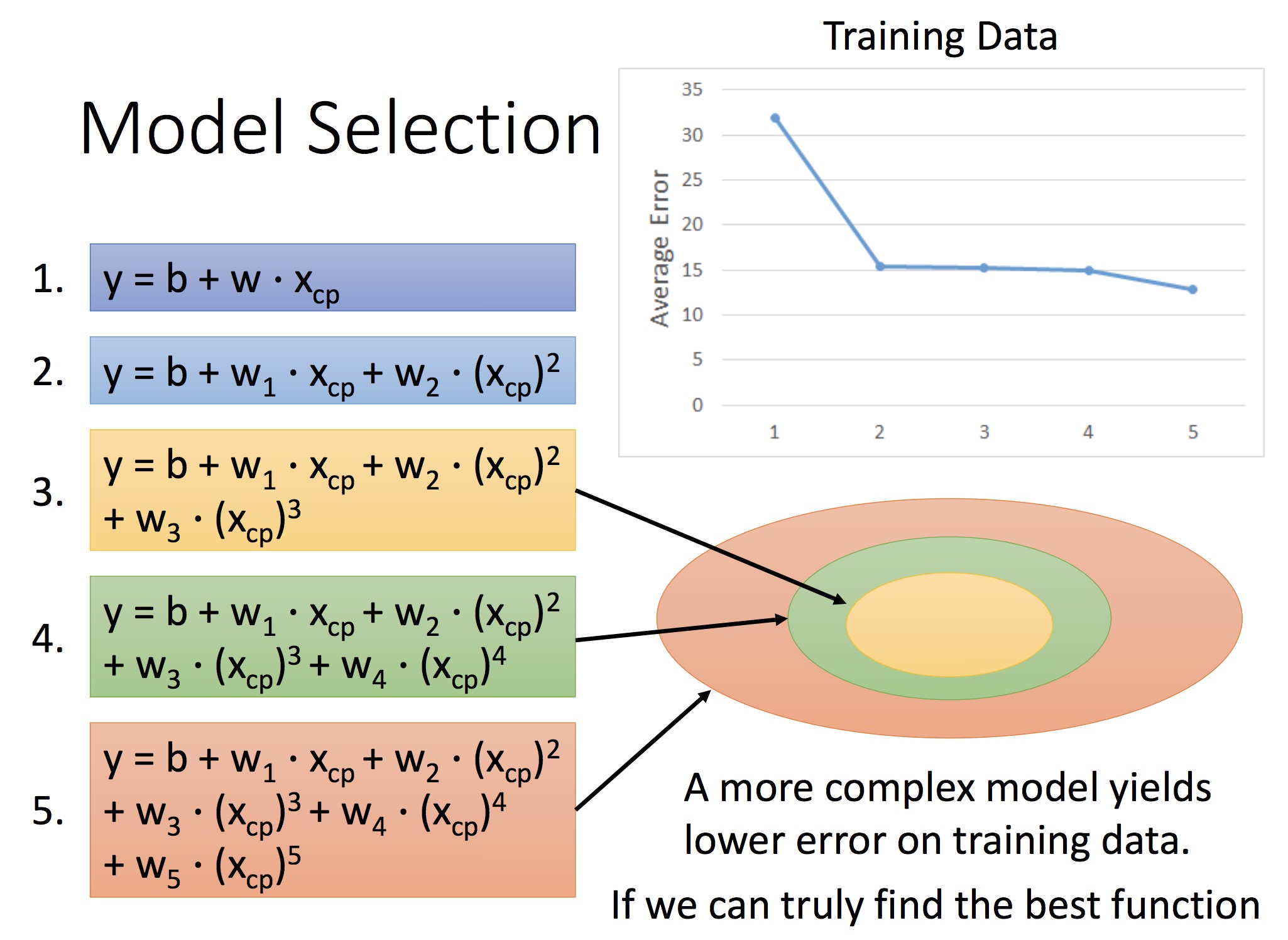
圆圈代表了模型的空间，模型次数越高，空间越大但误差也越大

所以要选择合适的 Model：

再考虑物种的情况，加入 Xs。预测与决策的内容（4-5: 含虚变量的回归）Xs 相当于一个决定截距的虚变量

本节的话除了思想，基本都是很基本的知识.

Regularition

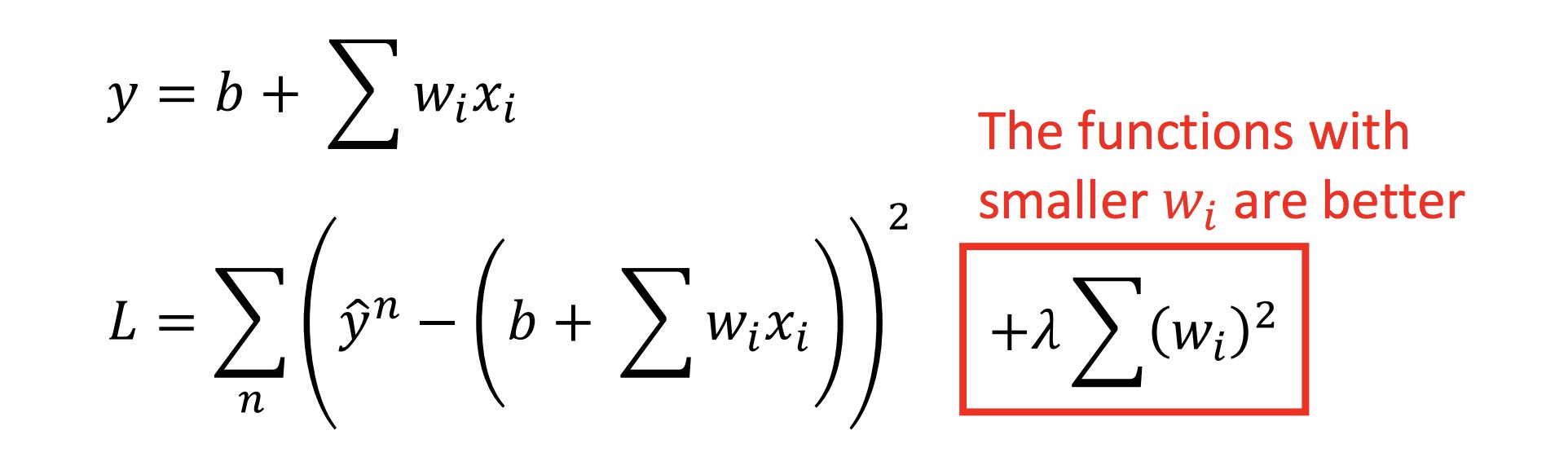
确定 Loss function 时，除开 error 项（第一项），往往加上第二项，这样确定下来的拟合函数系数可以尽量小，函数也会更加平滑：

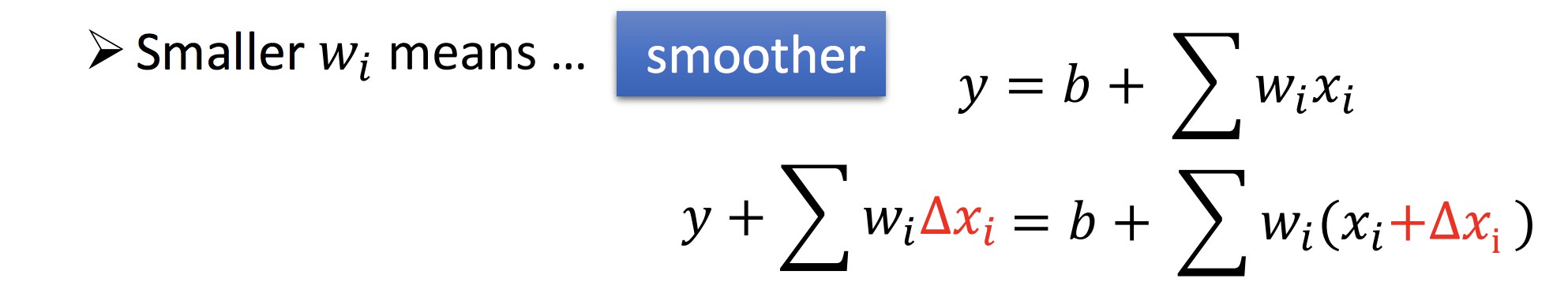
λ 的选取：

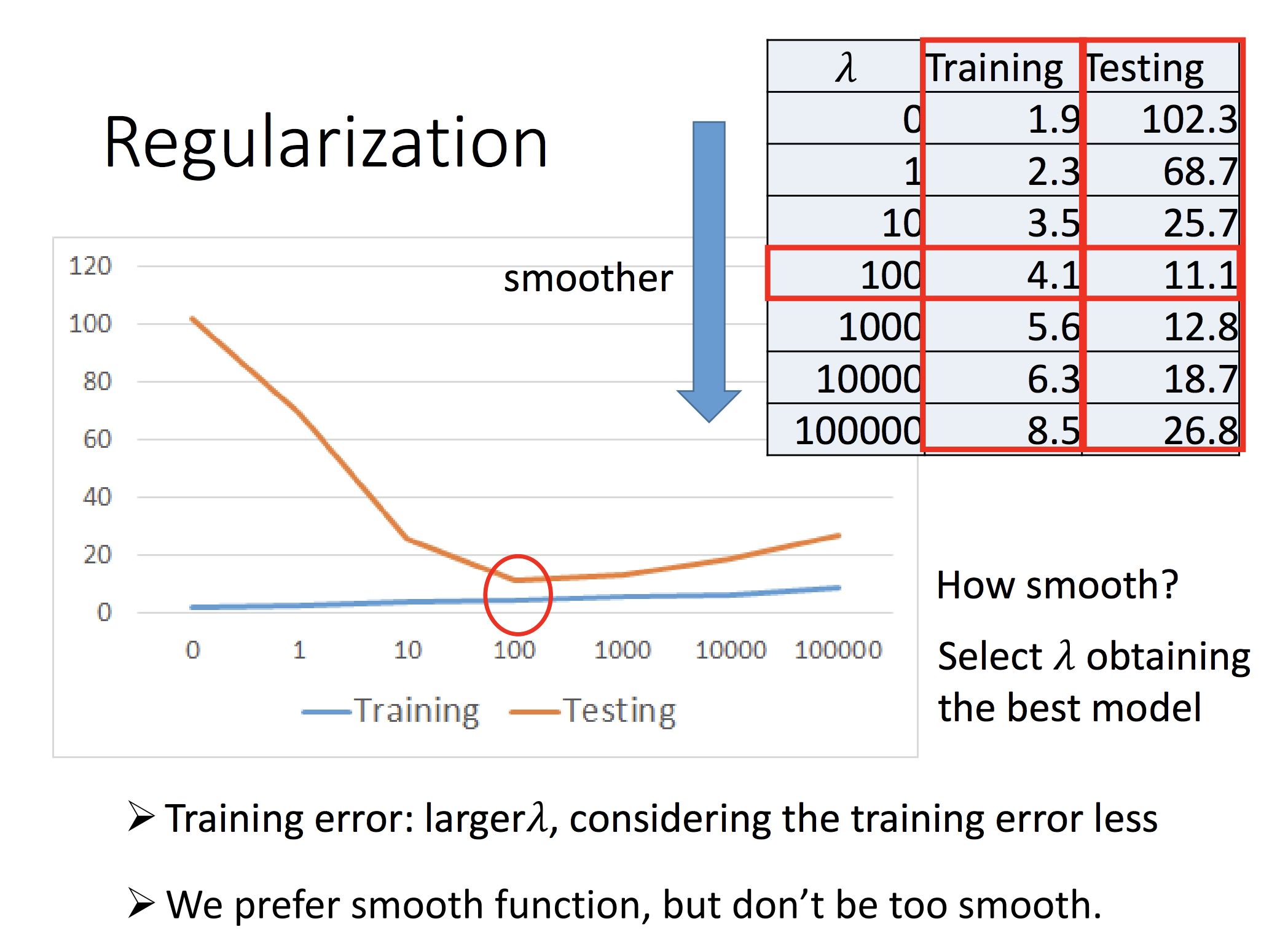
合适即可

总结：

Demo：

演示了梯度下降法逼近最优解的过程

Lecture 2: Error 来源 - Model 选取

数据误差的构成：

表现在 Loss Function 函数上：

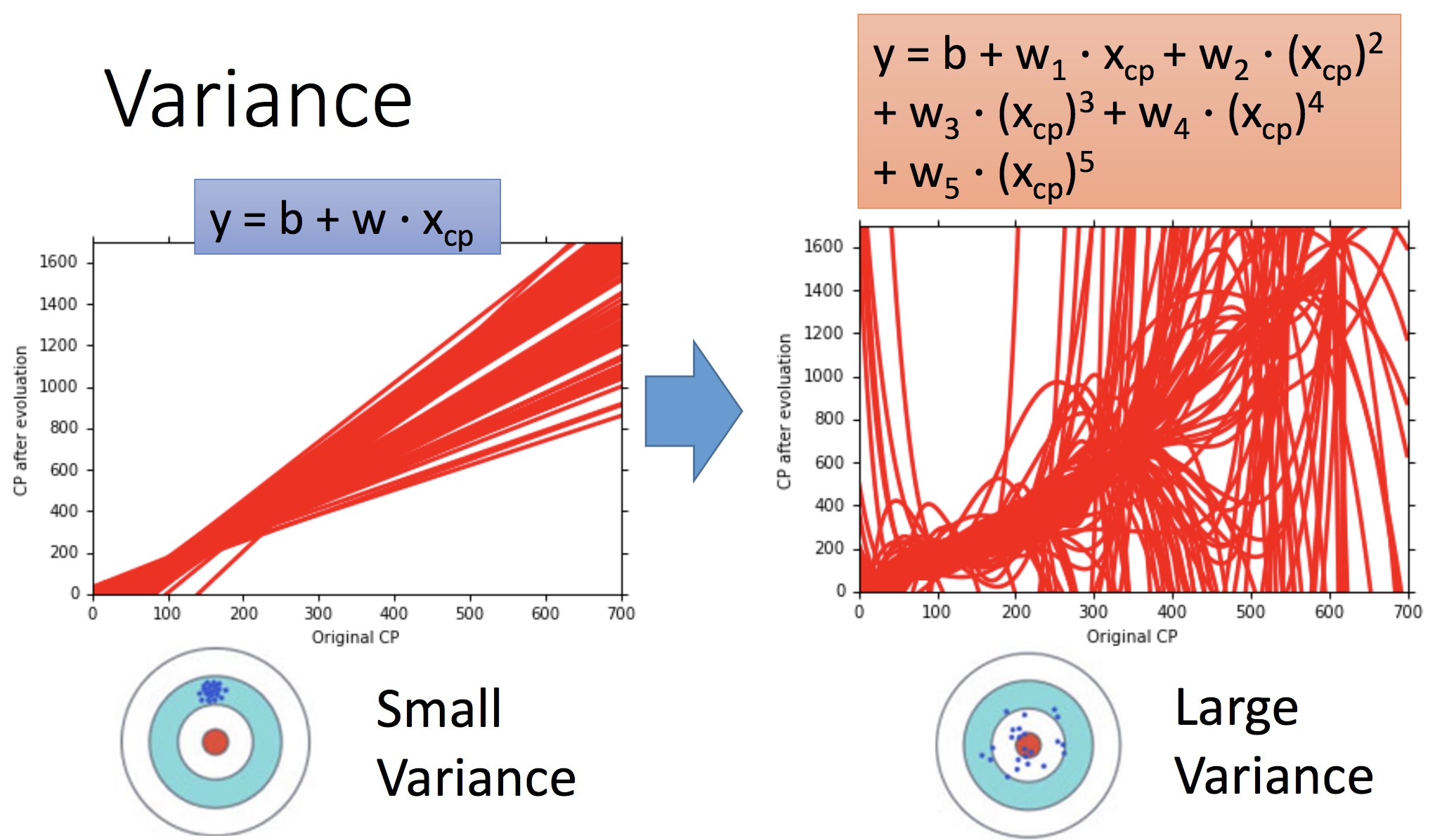
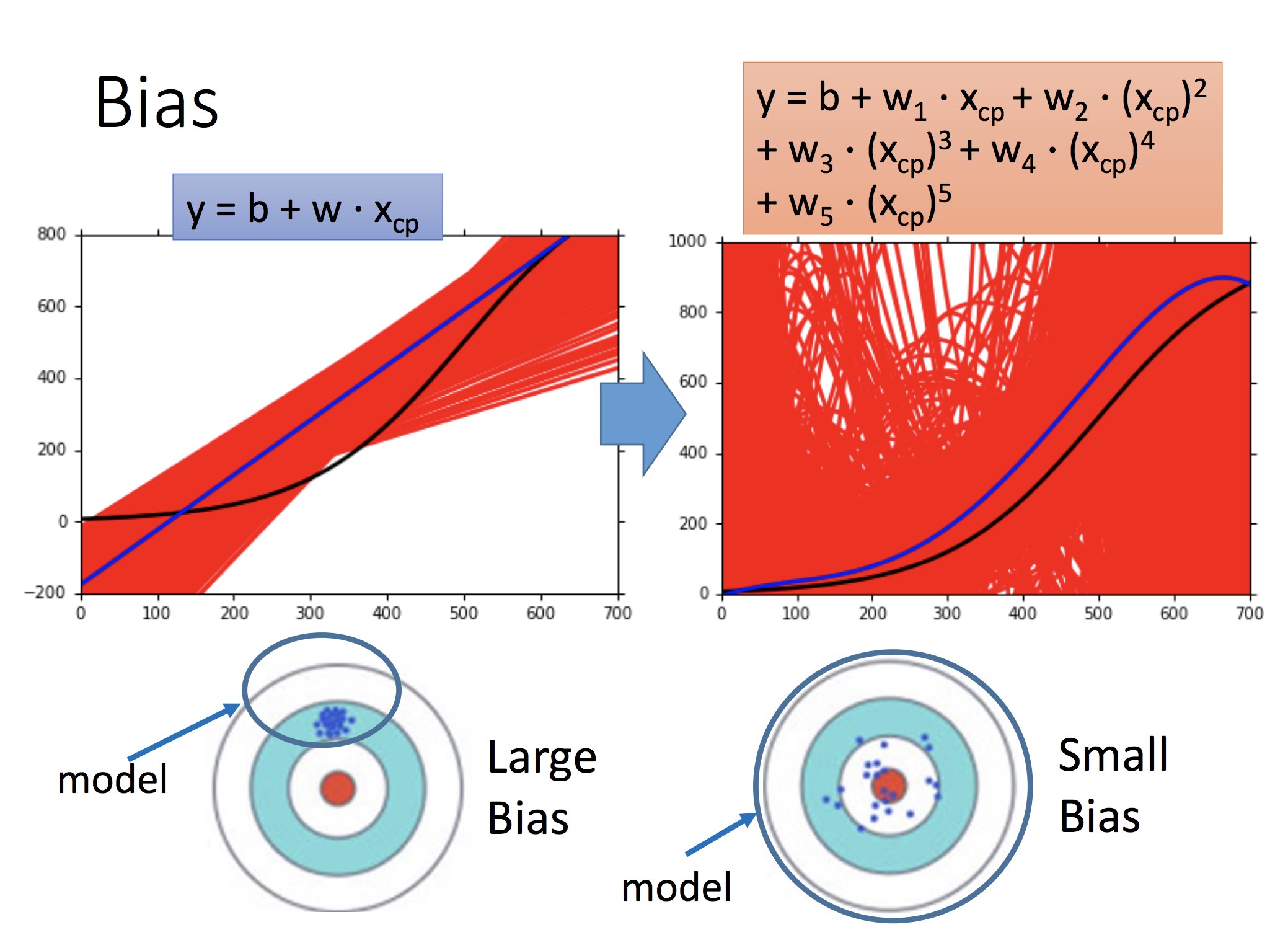
1: 分布较为集中（方差小），但是距离 f hat 还是有距离，偏差较大 = 代表简单的 Model

2: 分布散乱（方差大），但是偏差小 = 代表复杂的 Model

蓝色圈：最初选定的 Model set 集合。例如，采用一次回归注定了这个 set 的偏差较大

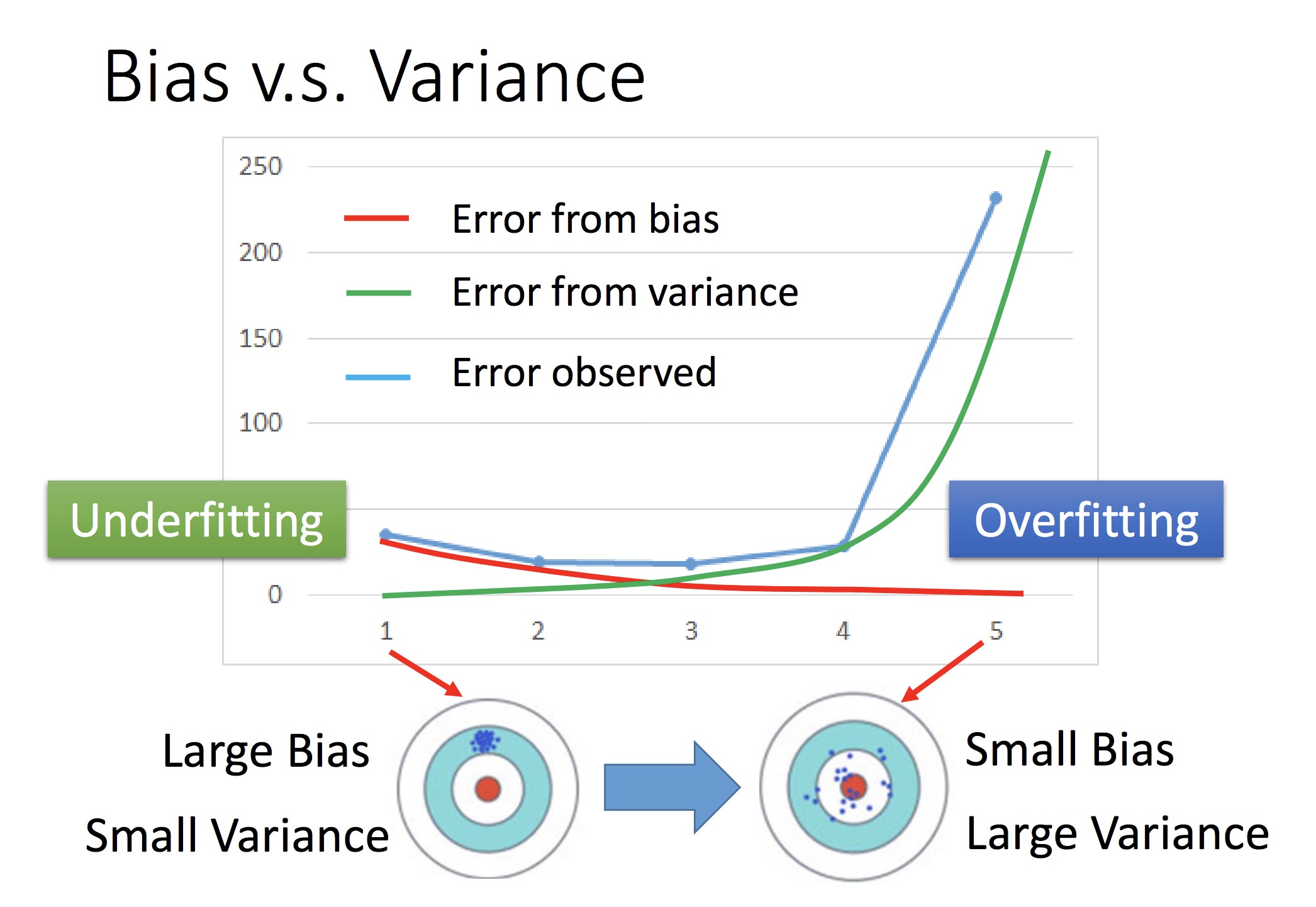
随着模型次数增加，偏差会越来越小（瞄得越来越准），但是分布会更加散乱

同时考虑的时候，可以得到蓝色的线，采取最合适的点代表的模型

如何减小误差

对 Bias：• Add more features as input • A more complex model

简单来讲就是换个好点的模型

对 Var： · 更多的训练数据 · 采用规范化（加上 λ（w𝙞）^2 项）

模型的选择上的问题：

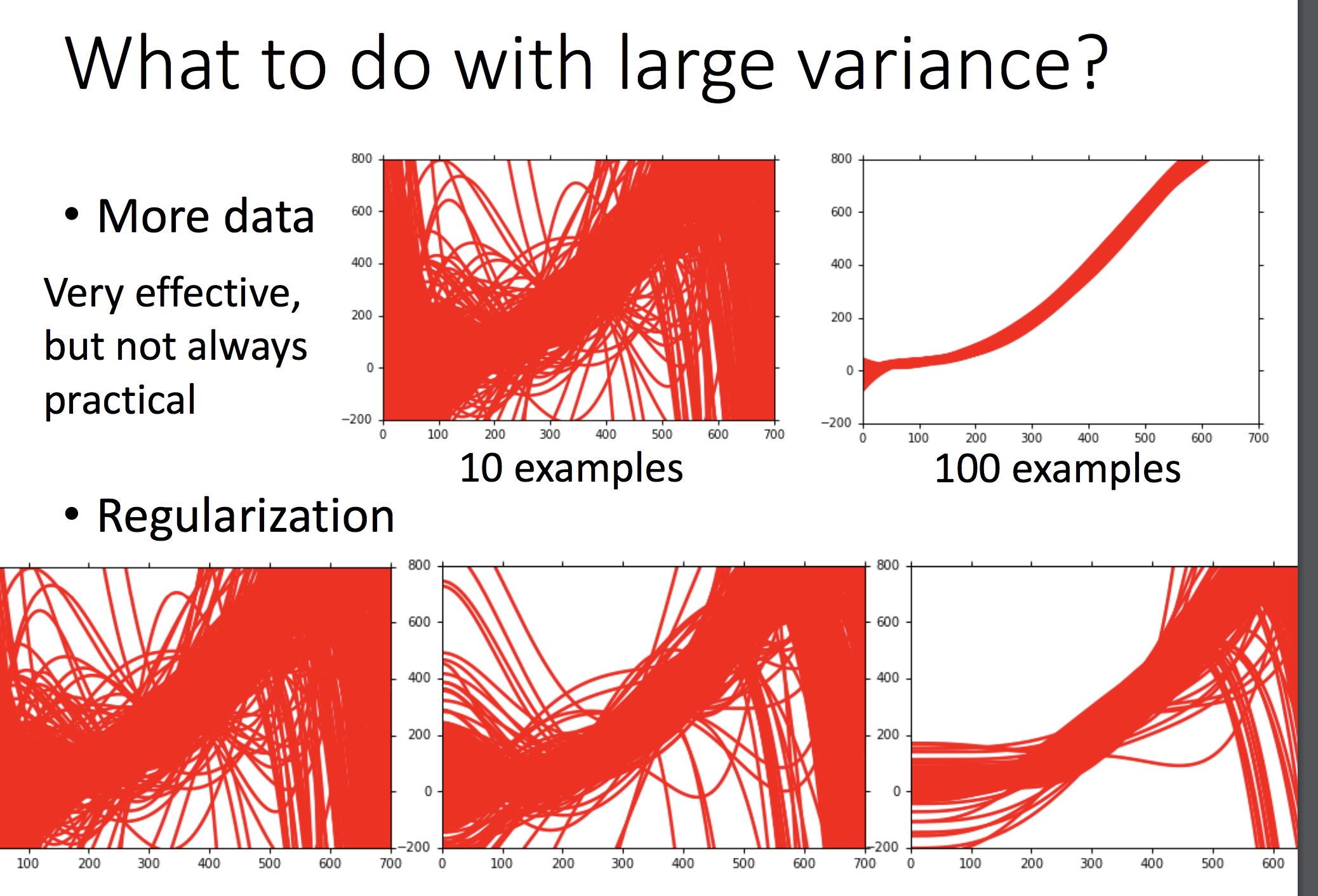
不应该：用手上已有的 Testing Set 去评价 model 好坏，因为真正的 Testing Set 全集是我们不具有的，真正的 set 下评价可能会不同

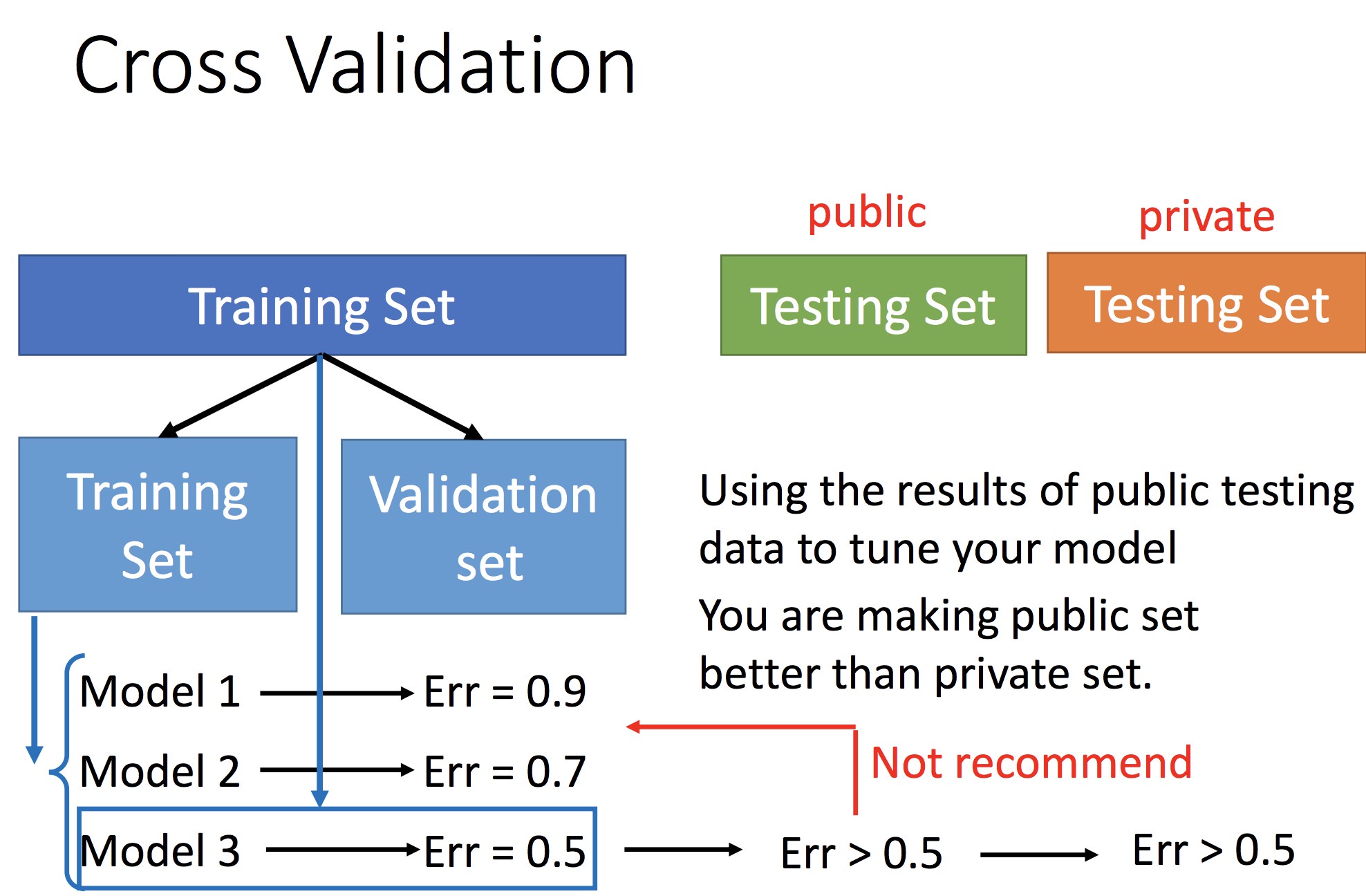
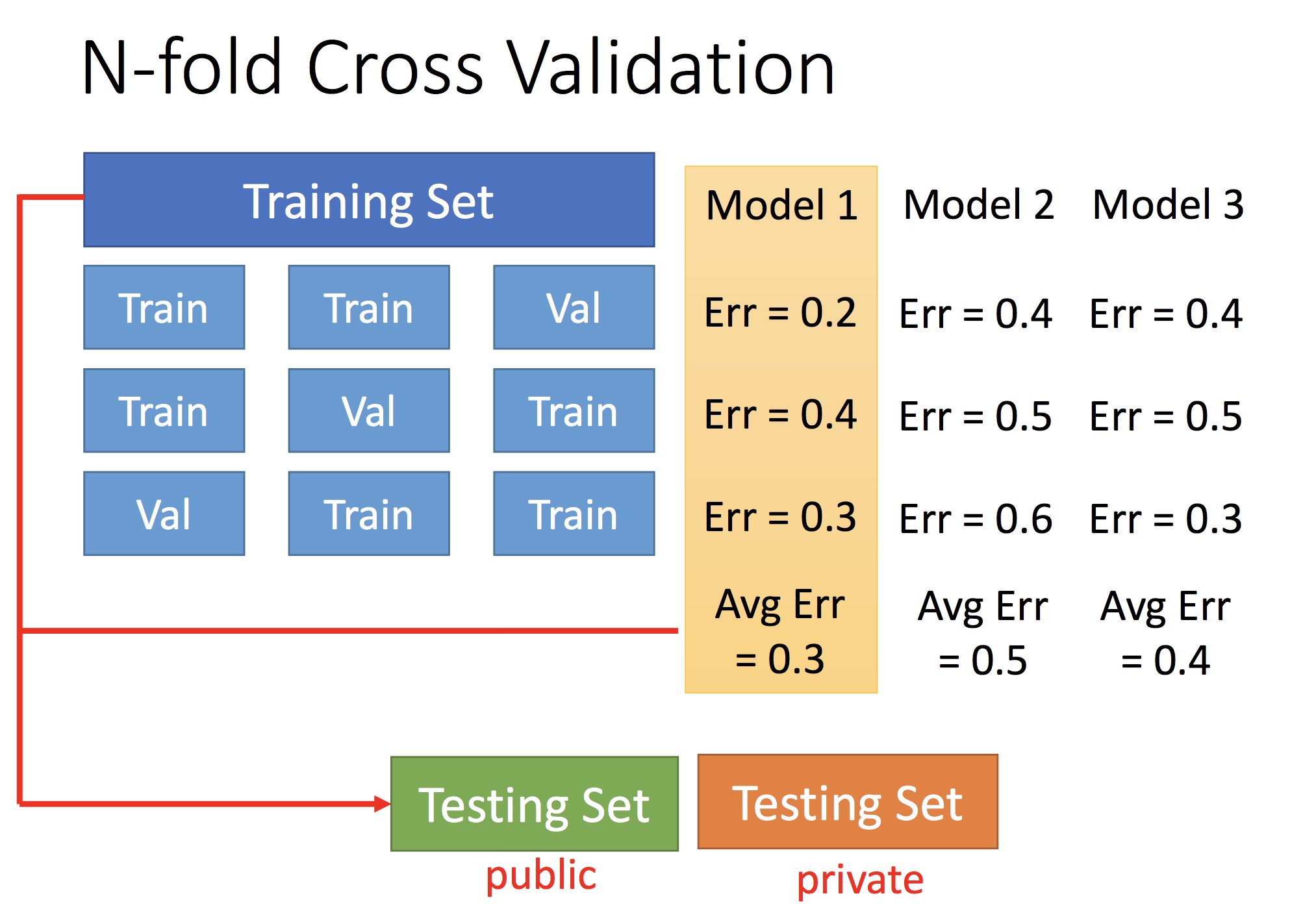
通过交叉验证确定最优 Model

两个 Demo：

1：表明局部最优和全局最优的关系

2：表明采用梯度下降法，说明存在 f 会不降反增的 case

HW0

前言

FIA 旗下最大的三个汽车运动赛事：F1，WEC，WRC。国际摩联旗下还有著名的moto GP。
我今年开始看的汽车运动赛事越来越多。也是对汽车运动越来越有兴趣。
在看的有 F1，F2，WEC，看得少的有 moto GP，戴那通，纳斯卡。

8102年了，供应链的控制能力还是决定厂商核心产品的因素。

之前的发刘海屏都还不敢吹嘘咋样咋样，华为p20这次发布会上把隐藏刘海当作一个“特性”还要拿出来讲…
我接触的人大多数都不喜欢刘海吧。不管是审美上还是功能上。iOS刘海没什么，虽然那么多UI元素被压缩在角落瑟瑟发抖，但是苹果是龙头，叫你适配你就必须适配，不然就下架app。安卓就不一样，各家自己做ROM，但是国际大厂都没有采用刘海屏，也没用魔改ROM来适配。